Problems

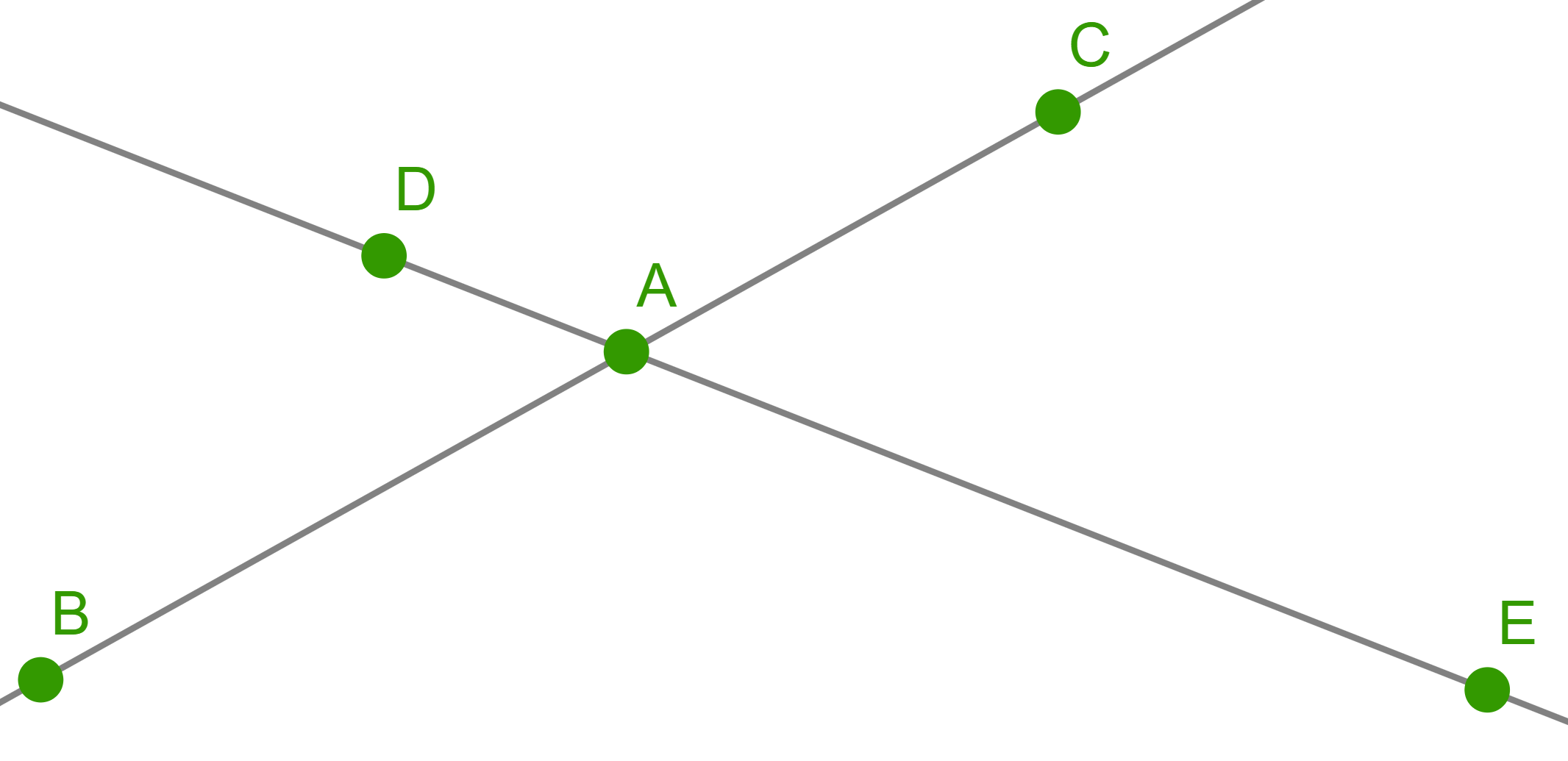
Five oaks are planted along two linear park alleys in such a way that there are three oaks along each alley, see picture. Where should we plant the sixth oak so that it will be possible to lay two more linear alleys, along each of which there would also be three oak trees growing?

Decipher the following puzzle. All the numbers indicated by the letter E, are even (not necessarily equal); all the numbers indicated by the letter O are odd (also not necessarily equal).

The smell of a flowering lavender plant diffuses through a radius of 20 m around it. How many lavender plants must be planted along a straight 400m path so that the smell of the lavender reaches every point on the path.

In a vase, there is a bouquet of 7 white and blue lilac branches. It is known that 1) at least one branch is white, 2) out of any two branches, at least one is blue. How many white branches and how many blue are there in the bouquet?

The angle at the top of a crane is \(20^{\circ}\). How will the magnitude of this angle change when looking at the crane with binoculars which triple the size of everything?

In some country there are 101 cities, and some of them are connected by roads. However, every two cities are connected by exactly one path.

How many roads are there in this country?

Determine all integer solutions of the equation \(yk = x^2 + x\). Where \(k\) is an integer greater than \(1\).

Prove that for every natural number \(n > 1\) the equality: \[\lfloor n^{1 / 2}\rfloor + \lfloor n^{1/ 3}\rfloor + \dots + \lfloor n^{1 / n}\rfloor = \lfloor \log_{2}n\rfloor + \lfloor \log_{3}n\rfloor + \dots + \lfloor \log_{n}n\rfloor\] is satisfied.

\(a_1, a_2, a_3, \dots\) is an increasing sequence of natural numbers. It is known that \(a_{a_k} = 3k\) for any \(k\). Find a) \(a_{100}\); b) \(a_{2022}\).

Given an endless piece of chequered paper with a cell side equal to one. The distance between two cells is the length of the shortest path parallel to cell lines from one cell to the other (it is considered the path of the center of a rook). What is the smallest number of colors to paint the board (each cell is painted with one color), so that two cells, located at a distance of 6, are always painted with different colors?