Problems

Using the representation of Latin alphabet as sequences of \(0\)s and \(1\)s five symbols long, encrypt your first and last name.

Decipher the quote from Philip Pullmans "His Dark Materials":
Erh csy wlepp orsa xli xvyxl, erh xli xvyxl wlepp qeoi csy jvii.
The same letters correspond to the same in the phrase, different letters correspond to different. We know that no original letters stayed in place, meaning that in places of e,r,h there was surely something else.

Decipher the quote from "Alice in Wonderland" from the following matrix:
\[\begin{array}{@{}*{26}{c}@{}} Y&q&o&l&u&e&c&d&a&i&n \\ w&a&r&l&a&w&e&a&t&y&k \\ s&n&t&c&a&e&k&c&e&a&m \\ t&o&d&r&w&e&a&t&a&h&r \\ a&c&n&t&n&e&o&d&t&r&h \\ n&i&d&n&l&g&m&e&x&s&z \end{array}\]

Decipher the following quote from Alice in Wonderland:
Lw zrxog eh vr qlfh li vrphwklqj pdgh vhqvh iru d fkdqjh.
The same letters correspond to the same in the phrase, different letters correspond to different. We know that no original letters stayed in place, meaning that in places of e,r,h there was surely something else.

Elon is studying the Twitter server. Inside the software he found two integer variables \(a\) and \(b\) which change their values when special search queries “RED”, “GREEN”, and “BLUE” are processed. More precisely the pair \((a, b)\) changes into \((a + 18b, 18a - b)\) when processing the query “RED”, to \((17a + 6b, -6a + 17b)\) when processing “GREEN”, and to \((-10a - 15b, 15a - 10b)\) when processing “BLUE”. When any of \(a\) or \(b\) reaches a multiple of \(324\), it resets to \(0\). If \((a, b) = (0, 0)\) the server crashes. On the server startup, the variables \((a, b)\) are set to \((20, 20)\). Prove that the server will never crash with these initial values, regardless of the search queries processed.

After mastering the Caesar shift cypher one may wonder how to generalize it. One possible way is to use Affine cypher. The difference between these two methods can be described as follows:

• In case of Caesar cypher we took a letter with position \(n\) from \(1\) to \(26\) and added to its position a number \(d\) obtaining the number \(n+d\), then we compute its residue modulo \(26\).

• In case of affine cypher we take a letter with position \(n\) and consider a number \(nx + d\) modulo \(26\).

To decipher such code we need to know values \(x\) and \(d\), then if we have a letter in the code with position \(m\), we can find \(n\) as \(n= (m-d)x^{-1}\) modulo \(26\). Here we have to explain what is \(x^{-1}\): for a number \(x < 26\) we are looking for such a number \(y\), that \(26\) divides \(xy-1\).

• Does there always exist a number \(x^{-1}\) modulo \(26\) for any \(x\)?

• Using data \(x=3\), \(d=8\) encrypt the word "SOLUTION".

Two expressions are written on the board:

\[1 + 22 + 333 + 4444 + 55555 + 666666 +7777777 + 88888888 + 999999999\] \[9 + 98 + 987 + 9876 + 98765 + 987654 + 9876543 + 98765432 + 987654321\]

Determine which one is greater or whether the numbers are equal.

Cut the "biscuit" into 16 congruent pieces. The sections are not necessarily rectilinear.

Bryn calls the date beautiful if all \(6\) digits of the date entry are different. For example: 19.04.23 is a beautiful date, but 19.02.23 and 01.06.23 are not. How many beautiful dates are there in \(2023\)?

In the middle of an empty pool there is a square platform of \(50 \times 50\) cm, split into cells of \(10\times 10\) cm. Sunny builds towers of \(10\times 10\times 10\)cm cubes on the platform cells. After that his friend Margo turns on the water and counts how many towers are still above the water level. They call each visible tower an island.

For example, let’s consider the case when the heights of the towers are as given in the table on the right. Then at the water level of \(5\) cm there is \(1\) island, at the water level of \(15\) cm there are two islands (if the islands have a common corner or don’t intersect at all, they are considered separate islands), and at the water level of \(25\) cm, all the towers are covered with water and there are \(0\) islands.

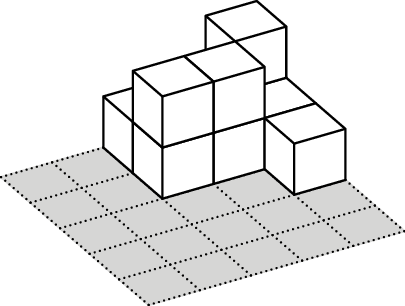
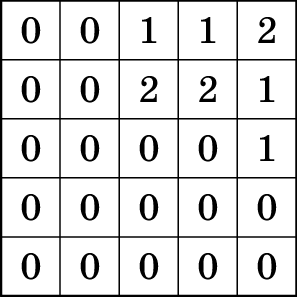
Find out how Sunny should build his towers to get the following numbers of islands corresponding to the level of water in the pool: \[\begin{array}{@{}*{26}{c}@{}} \textit{Water level (cm)}& 5& 15& 25& 35& 45\\ \textit{Number of islands}& 2& 5& 2& 5& 0 \end{array}\]

In the solution, write down how many cubes are there composing a tower in each cell as it is done in the example.