Problems

Seven Smurfs live in seven mushroom houses. There is a tunnel between every pair of houses, so from any house you can walk to any other house. One of the Smurfs, Clumsy, starts walking from his house, but he must not use the same tunnel more than once. He keeps walking until he reaches a house where all the tunnels have already been used. Where will Clumsy’s journey end?

Welcome back from the summer holidays! We hope you’re rested and ready for an exciting year of problems. Today we’re going to dive right into our first topic with a fun game called “Lights Out."

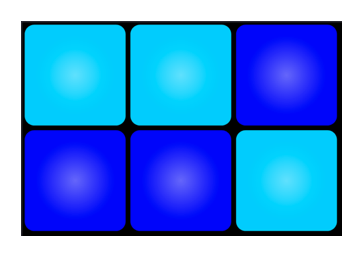
Imagine a board of little square buttons, and each square has a light that can be either on or off. When you press on a square, that square’s light flips (from on to off, or off to on), but so do the lights of all its neighbours: the squares directly above, below, to the left, and to the right of it. In the pictures of today’s problem sheet, we’ll use dark blue to mean that a light is on, and light blue to mean that the light is off. An interactive version of this game can be freely found by searching ’Lights Out (game)’ on Wikipedia. It may be useful if you want to try some of the harder problems at home.

Let’s see what kind of games we can play with these boards:

Imagine a \(2\times 2\) “Lights Out" board. If every light is off at the start, how can we turn on just one of the squares? Can you notice something about the order in which we press squares?

Suppose we have a \(2\times 2\) board where all the lights start being turned off, how can we turn on the top two lights?

A \(2\times 2\) "Lights Out" board starts with all the light being turned off. How can you turn on the top-left and bottom-right squares at the same time?

Now let’s imagine a \(3\times 3\) board, how can you turn on just the middle light?

A very important tool in maths is to use symmetries to make problems easier. For today, define a symmetry of a shape as a movement that leaves the shape looking exactly the same as initial. For example, rotating a square by \(90^\circ\) (spinning it by a quarter turn) is a symmetry. Imagine you are playing lights out on a board that has no quiet plans. Explain why if a light pattern has a certain symmetry, then its corresponding plan will also have the same symmetry.

A \(3\times 3\) “Lights Out" board starts with all the lights off. Explain why \(5\) is the smallest number of presses you need to turn the whole board on.

Imagine a “Lights Out” board that starts with all the lights off. A plan that is not empty (it has at least one button in it) is called quiet if, after pressing all the buttons in the plan, the board ends up all off again (remember that plans can’t have buttons being pressed twice). Now take a \(3\times 2\) “Lights Out” board. Can you find two different ways to turn every light on? How can this help you to discover a quiet plan?

Let’s now play with the \(2\times 3\) “Lights Out’’ board. You can take it as a fact that there are exactly \(3\) quiet plans for this board (you can read example \(3\) again to remind yourself of quiet plans). Can you find them all? Using this, or otherwise, can you work \(4\) plans that produce the following pattern?