Problems
Once again consider the game from Example 2.
(a) Will you change your answer if the field is a rectangle?
(b) The rules are changed. Now you win if the sum of numbers in each row is greater than 100 and the sum of the numbers in each column is less than 100. Is it possible to win?
The text for this problem was originally typed in three different fonts and in three different colours. The original style is lost now, and Bella and Louise disagree on the following. Bella says that whatever the original font was it was always possible to choose three letters from the text such that all the three colours and all the three fonts were presented in that triple, and Louise does not think so. Who is right?
a) A bachelor student Peter haven’t slept properly for the last month. One of the reasons for that among many others was that every Monday at 3 p.m. he had a deadline for submitting his weekly calculus assignments. During the first month he counted six deadlines. Can it be the case or would you advise him to have more sleep?
(b) Once Peter checked the table with the assignment results he realized there were fewer Mondays in the last month. Is it possible there were only five Mondays?
(a) A picnic spot has a form of a 100 m\({}\times {}\)100 m square. Is it possible to partially cover it with non-intersecting square picnic blankets so that the total sum of their perimeters will be greater than 10,000 m?
(b) One sunny day almost every citizen came to the picnic spot from point (a). All of them brought square picnic blankets. In a local newspaper there was mentioned that the total area of grass covered with picnic blankets was greater than 20,000 m\(^2\). Do you think it was possible or did they make a mistake in their computations?
Scrooge McDuck has 100 golden coins on his office table. He wants to distribute them into 10 piles so that no two piles contain the same amount of coins. And moreover, no matter how you divide any of the piles into two smaller piles among the resulting 11 piles there will be two with the same amount of coins. Sounds impossible? Try to find a suitable example. Scrooge spent a while on working out this question, maybe he will even give you a penny.
Express the number 111 as a sum of 51 natural numbers so that each of the terms has the same sum of digits.
There are 36 parcels weighing 1 kg, 2 kg, 3 kg, ..., 36 kg. Today only three cars are in service. Each car has a capacity of 12 parcels. Can one distribute all packages between the cars in such a way that each vehicle has the same total weight of parcels?
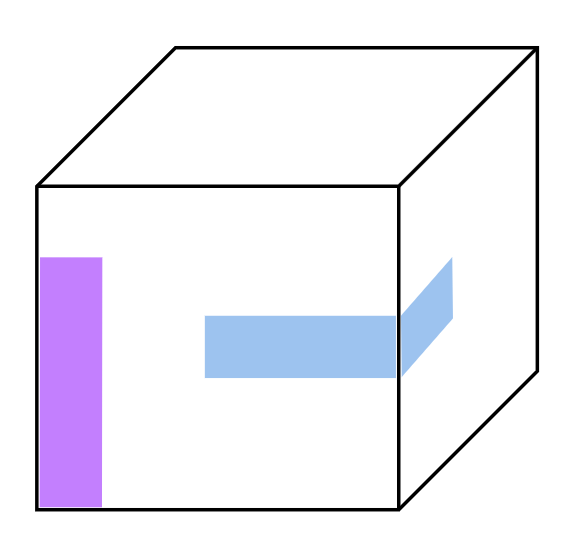
Imagine you have a cube (a box with six square sides). First, cut 16 identical colourful rectangular paper strips of any size you like (choose one size and make all 16 the same). Can you cover the entire outside surface of the cube with these strips, with no gaps and no overlapping? The strips may bend and wrap around edges and corners, but after cutting the 16 strips, you are not allowed to cut them again, and everything must stay on the cube’s surface. Is it possible? Explain why or why not. (For example, two of the strips may look like this:
a) Express the number 221 as a sum of 52 natural numbers so that each of the terms has the same sum of digits.
(b) Express the number 226 as a sum of 52 natural numbers so that all terms have the same sum of digits.
a) In the context of Example 2 assume we have some number of parcels each weighing different amount of kilograms. We still have 3 identical cars of equal capacities (in numbers of packages) and we still want to distribute parcels in such a way that each car has the same total weight of parcels. Knowing that the number of parcels is not greater than 100 find the maximum and the minimum amounts of packages for which it is possible.
(b) Now we have 3 trucks so we do not really care about the sizes of parcels and their number. But yet we need to satisfy the condition of equal total weights of parcels in each vehicle. Can we do so if there are 27 packages weighing 1 kg, 2 kg, ..., 27 kg?