Problems

In the trapezium \(ABCD\) the point \(E\) is the point of intersection of the sides \(AB\) and \(CD\), the point \(G\) is the point of intersection of diagonals, the points \(F,H\) are the midpoints of the sides \(BC\) and \(AD\) respectively.

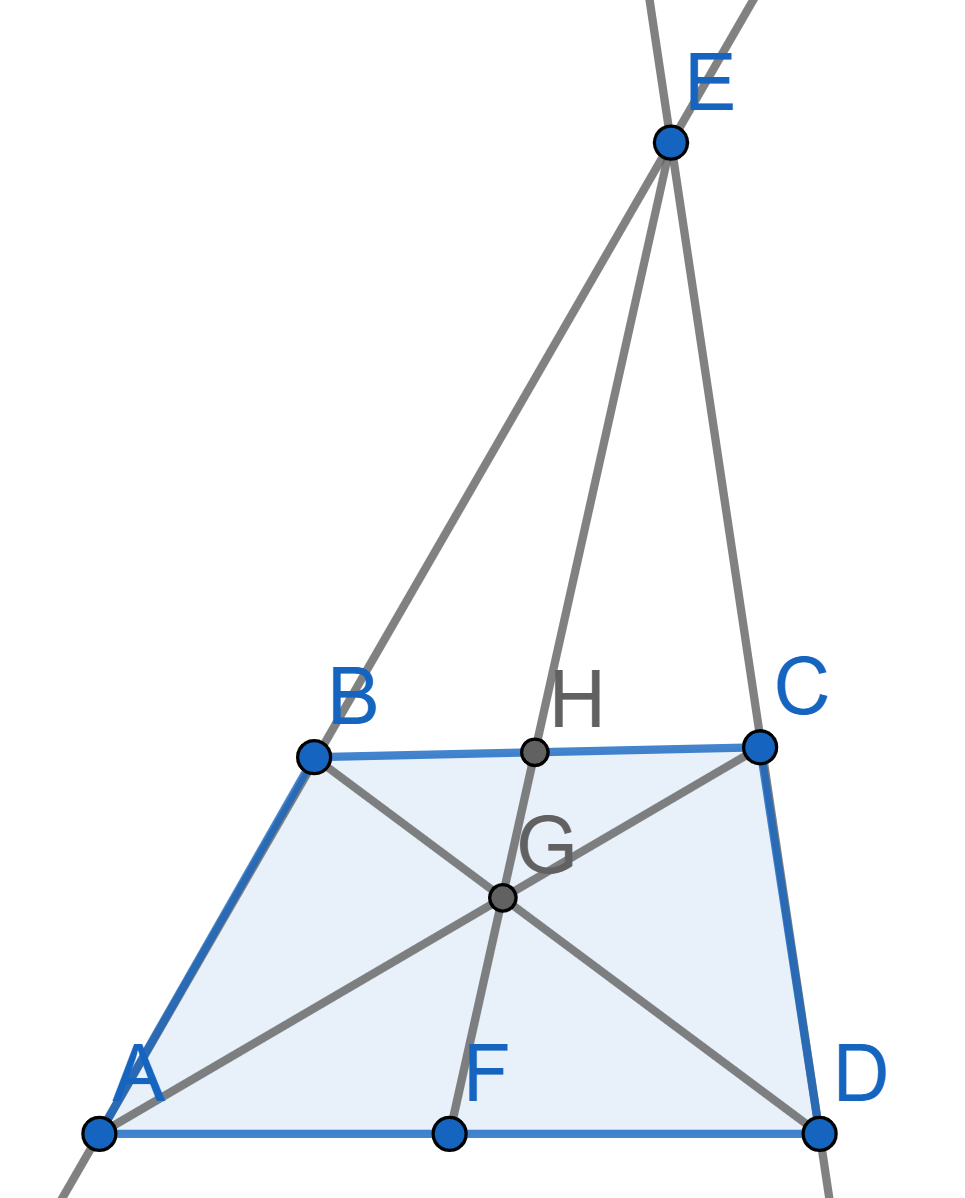
Prove that the points \(E,F,G,H\) lie on one line.

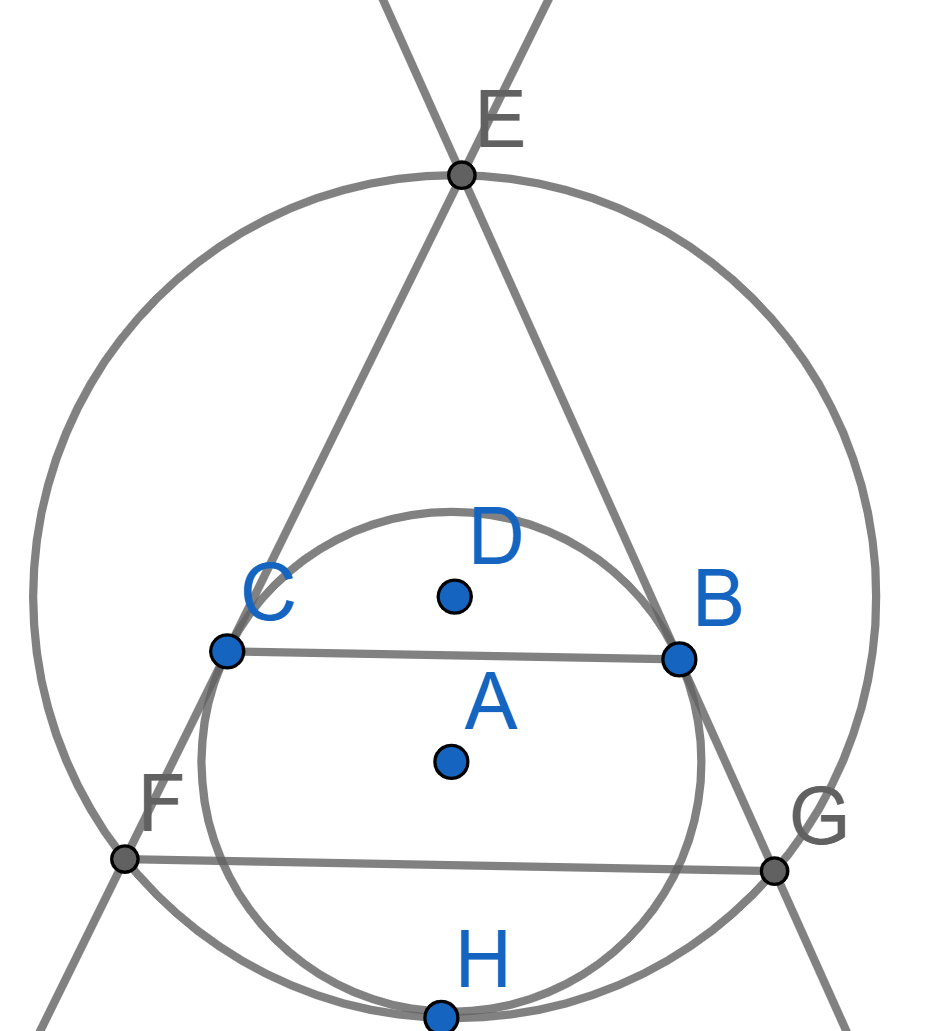
The triangle \(EFG\) is equilateral and \(EF=EG\). A circle with center \(A\) is tangent to the sides \(EF\) and \(EG\) at the points \(C\) and \(B\) respectively. It is also tangent to the circle circumscribed around the triangle \(EFG\) at the point \(H\). Prove that the midpoint of the segment \(BC\) is the center of the circle inscribed into he triangle \(EFG\).

Prove that under the homothety transformation a polygon is transferred into a similar polygon. I.e. homothety preserves angles and ratios.

Remember that a still-life in the Game of Life was a pattern that did not change after any number of steps. Show that the following pattern can not be turned into a still life by only changing dead cells into alive cells.

Is it possible to arrange \(10\) numbers in a row such that:

• The sum of any \(4\) consecutive numbers is positive.

• The sum of any \(5\) consecutive numbers is positive.

• The sum of any \(7\) consecutive numbers is negative?

In how many different ways can you place \(12\) chips in the squares of a \(4\times 4\) chessboard so that

1. there is at most one chip in each square, and

2. every row and every column contains exactly three chips?

On a TV screen the number \(1\) appears. Every minute that passes by, the number that is currently on the screen increases by the sum of its digits. For example: if at some point the number \(12\) appears on the screen, the next number will be \(12+(1+2)=15.\) Will the number \(123456\) ever appear on the screen?

Seven vertices of a cube are labelled with the number \(0\), and the remaining vertex is labelled with \(1\). You are allowed to repeat the following move: choose an edge of the cube and increase by \(1\) the numbers at both ends of that edge.

Is it possible to reach eight numbers that are all divisible by three?

Each number on the number line (not only whole numbers!) is painted black \((B)\) or white \((W)\). Is it always possible, regardless of how the number line is painted, to find a line segment such that both its endpoints and its middle point are painted with the same colour?

A book club with 37 members is reading the following books: “Brave New World", “Dracula" and “Flatland". Each member chose one of the books, though some people chose more than one book. We know that:

1. 23 people chose “Brave New World";

2. 18 people chose “Dracula";

3. 26 people chose “Flatland";

4. 7 people chose all three books.

How many people chose at least two books?