Problems

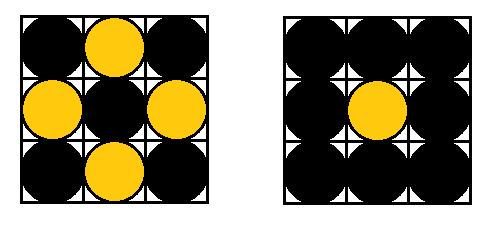
Nine lightbulbs are arranged in a \(3 \times 3\) square. Some of them are on, some are off. You are allowed to change the state of all the bulbs in a column or in a row. That means all the bulbs in that row or column that were initially off now light up, and the ones that were initially on, now go dark. Is it possible to go from the arrangement in the left to the one on the right by repeating this operation?

Anna’s sister, Claire, has \(10\) novels, \(11\) textbooks and \(12\) comic books on her shelf. She also doesn’t like to keep all her books there. Each time she takes two books of different type from the shelf and puts a book of the third type back on. For example, she might take a novel and a comic book and put a textbook back. Show that eventually there are only textbooks left on her shelf.

All the squares of a \(9 \times 9\) chessboard were coloured black and white in a traditional way, such that the corner squares are all white. With each move you can choose two neighbouring squares and change both of their colours - black to white and white to black. Can you reach a chessboard that is all black in this way? (Squares that are one diagonal away also count as being neighbors)

A rook in chess can move any number of squares in the same row or column. Let’s invent a new figure, a "little rook" that can only move one square in each of these directions. If we start with the "little rook" in the bottom right corner of an \(8 \times 8\) chessboard, can we make it to the top left corner while visiting each square exactly once?

There are \(15\) lightbulbs in a row, all switched off. We can pick any three of them and change their state. Can we repeat this operation an even number of times such that at the end all the lightbulbs are on?

There are numbers \(1,2,3,4,5,6,7,8,9\) and \(10\) written on a board. Each time you make a "move" you can erase three of the remaining numbers, \(a,b\) and \(c\), and replace them with the numbers \(2a+b,2b+c\) and \(2c+a\). Is it possible to make all the \(10\) numbers left on the board equal?

On a certain island there are \(17\) grey, \(15\) brown and \(13\) crimson chameleons. If two chameleons of different colours meet, both of them change to the third colour. No other colour changes are allowed. Is it possible that after a few such colour transitions all the chameleons have the same colour?

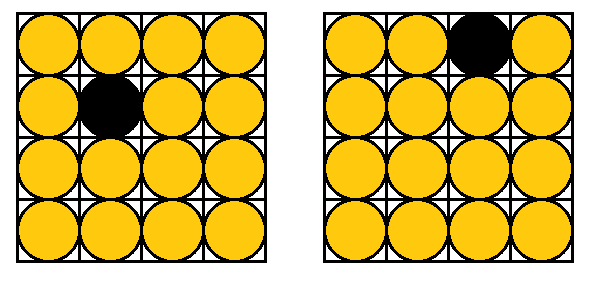
Sixteen lightbulbs are arranged in a \(4 \times 4\) grid. Some of them are on, the other ones are off. You are allowed to change the state of all the bulbs in a column, in a row, or along any diagonal (note: there are \(14\) diagonals in total!). Is it possible to go from the arrangement on the left to the one on the right by repeating this operation?

The numbers \(1\) to \(2025\) are written on a board. In one move we can erase two numbers and replace them with the absolute value of their difference. Can we achieve a sequence consisting of only \(0\) after some number of moves?

Sometimes a problem describes a certain process and asks you whether a certain result can be achieved through a series of repeated actions. How could we prove that such a result is impossible to obtain? One of the ways is to observe all the properties of the process that do not change after performing some action, or alternatively, properties that change in a predictable way. We call these properties "Invariants".