Problems
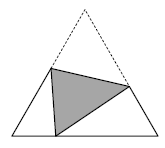
A equilateral triangle made of paper bends in a straight line so that
one of the vertices falls on the opposite side as shown on the picture.
Show that the corresponding angles of the two white triangles are
equal.
In how many ways can you read the word TRAIN from the picture below, starting from T and going either down or right at each step?

There are \(100\) people in a room. Each person knows at least \(67\) others. Show that there is a group of four people in this room that all know each other. We assume that if person \(A\) knows person \(B\) then person \(B\) also knows person \(A\).
The numbers \(a\) and \(b\) are integers and the number \(p \ge 3\) is prime. Suppose that \(a+b\) and \(a^2 +b^2\) are divisible by \(p\). Show that \(a^2 + b^2\) is divisible by \(p^2\).
There are \(33\) cities in the Republic of Farfarawayland. The delegation of senators wants to pick a new capital city. They want this city to be connected by roads to every other city in the Republic. They know for a fact that given any set of \(16\) cities, there will always be some city that is connected by roads to all those selected cities. Show that there exists a suitable candidate for the capital.
John drunk a \(\frac16\) of a full cup of black coffee and then filled the cup back up with milk. Then he drunk a third of what he had in the cup. Then, he refilled it back to full with milk again, and after that, drunk a half of the cup. Finally, he once again refilled the cup with milk and drunk everything he had. What did he drink more of - coffee or milk?
A round necklace contains \(45\) beads of two different colours: red and blue. Show that it is possible to find two beads of the same colour next to each other.
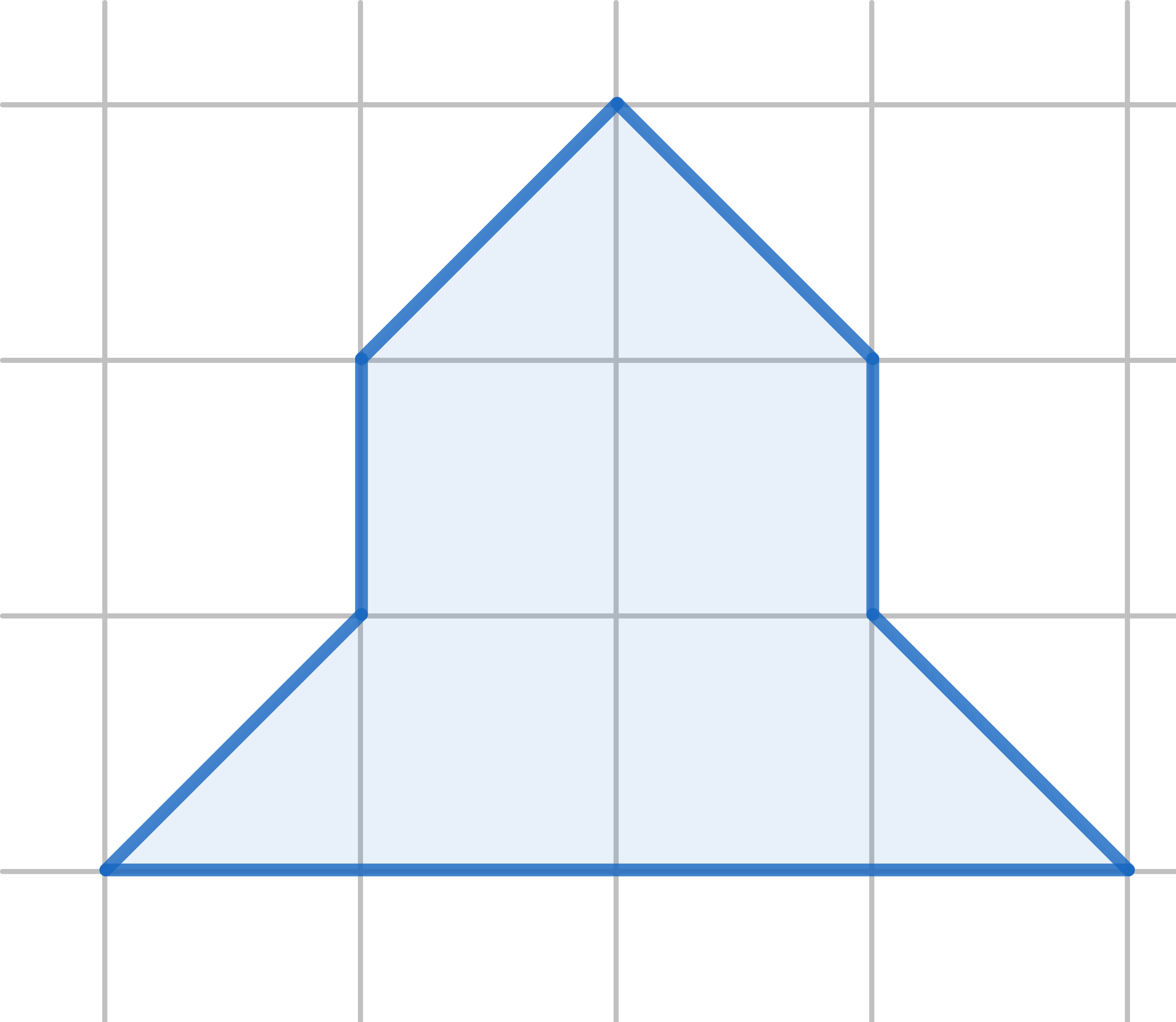
Cut this figure into \(4\) identical shapes. (Note: you have to use the entire shape. Rotations and reflections count as identical shapes)
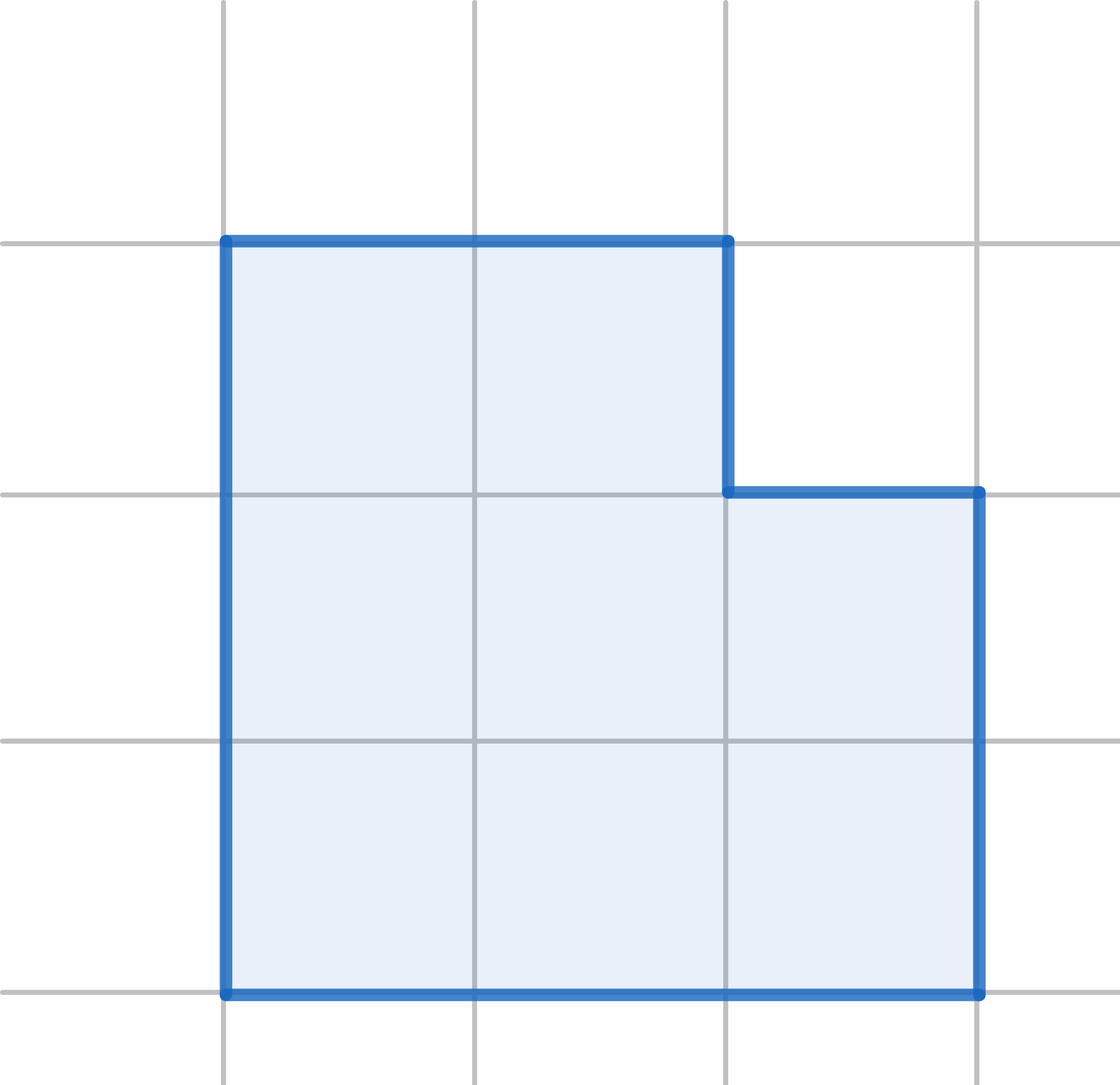
The diagram shows a \(3 \times 3\) square with one corner removed. Cut it into three pieces, not necessarily identical, which can be reassembled to make a square:
Find all possible non-zero digits \(A\) for which the following holds \((AA+AA+1) \times A = AAA\). (Recall \(AA\) means the two-digit number whose first and second digits are \(A\))