Problems
Can you cover a \(10 \times 10\) board using only \(T\)-shaped tetrominos?
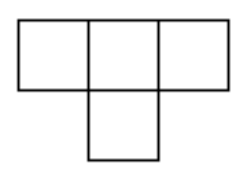
Can you cover a \(10 \times 10\) square with \(1 \times 4\) rectangles?
Two opposite corners were removed from an \(8 \times 8\) chessboard. Is it possible to cover this chessboard with \(1 \times 2\) rectangular blocks?
One unit square of a \(10 \times 10\) square board was removed. Is it possible to cover the rest of it with \(3\)-square \(L\)-shaped blocks?
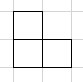
A \(7 \times 7\) square was tiled using \(1 \times 3\) rectangular blocks in such a way that one of the squares has not been covered. Find all the squares that could be left without being covered.
Can you cover a \(13 \times 13\) square using \(2 \times 2\) and \(3 \times 3\) squares?
Is it possible to cover a \(10 \times 10\) board with the \(L\)-tetraminos without overlapping? The pieces can be flipped and turned.
On a \(9\times 9\) board \(65\) bugs are placed in the centers of some of the squares. The bugs start moving at the same time and speed to a square that shares a side with the one they were in. When they reach the center of that square, they make a \(90\) degrees turn and keep walking (without leaving the board). Prove that at some moment of time there are two bugs in the same square. Note: When they turn it can be either to the right or to the left.
A \((2n - 1) \times (2n - 1)\) board is tiled with pieces of the following possible types:
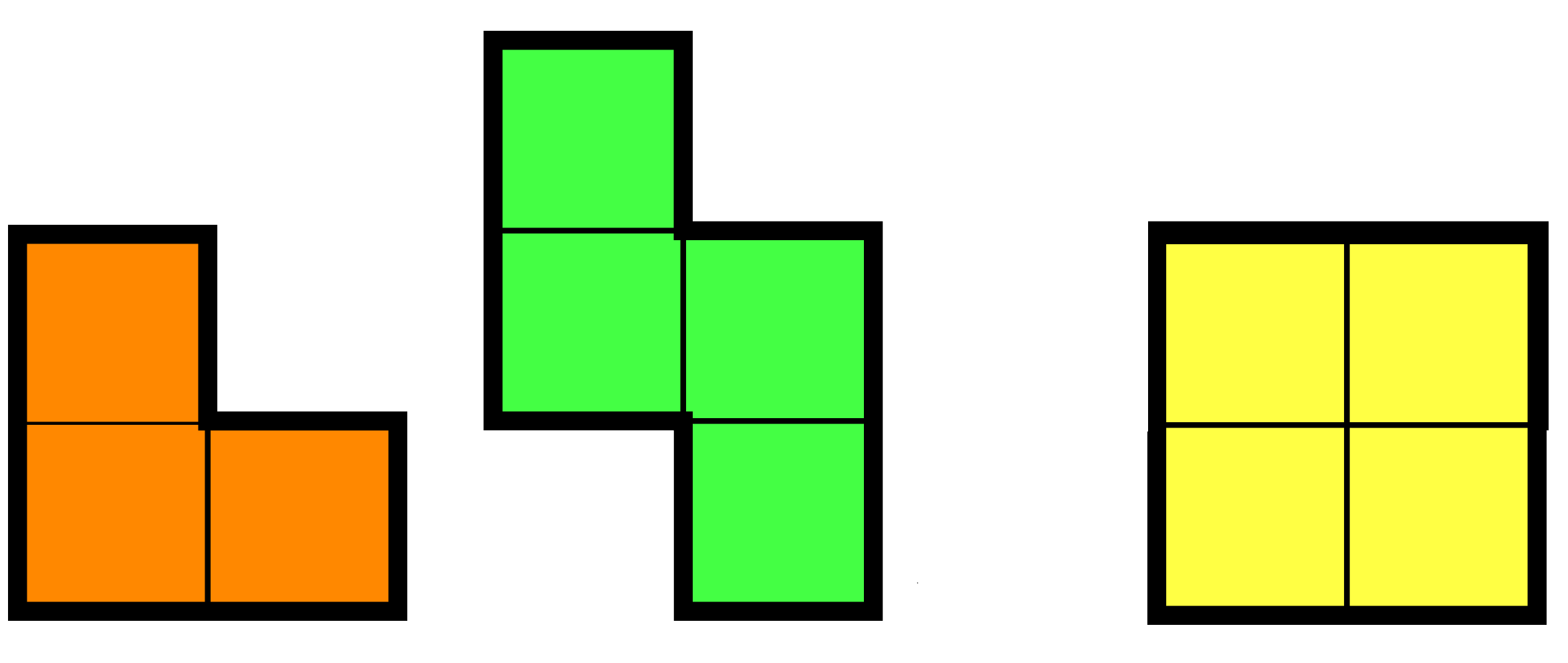
Prove that at least \(4n-1\) of the first type have been used.
In an \(n \times n\) board the squares are painted black or white in some way. Three of the squares in the corners are white and one is black. Show that there is a \(2\times 2\) square with an odd number of white unit squares.