Problems
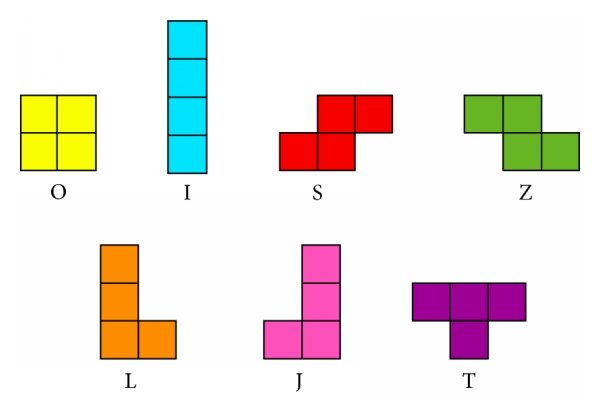
Consider the 7 different tetrominoes. Is it possible to cover a \(4\times7\) rectangle with exactly one copy of each of the tetrominoes? If it is possible, then provide an example layout. If it is not possible, then prove that it’s impossible.
We allow rotation of the tetrominoes, but not reflection. This means that we consider \(S\) and \(Z\) as different, as well as \(L\) and \(J\).
In the following grid, how many different ways are there of getting from the bottom left triangle to the bottom right triangle? You must only go from between triangles that share an edge and you can visit each triangle at most once. (You don’t have to visit all of the triangles.)
Two fractions sum up to \(1\), but their difference is \(\frac1{10}\). What are they?
On her birthday, my grandma was asked how old she was. She said: "Start with the year I was born. Add the current year to it. Then, from the sum subtract the year I celebrated by \(20\)th birthday. From that, take away the year I was \(30\). The result will be \(16\)." How old is my grandma?
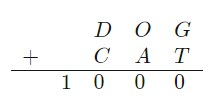
In the long addition above, each letter corresponds to a different digit. What is the sum \(D + O +G + C +A +T\)?
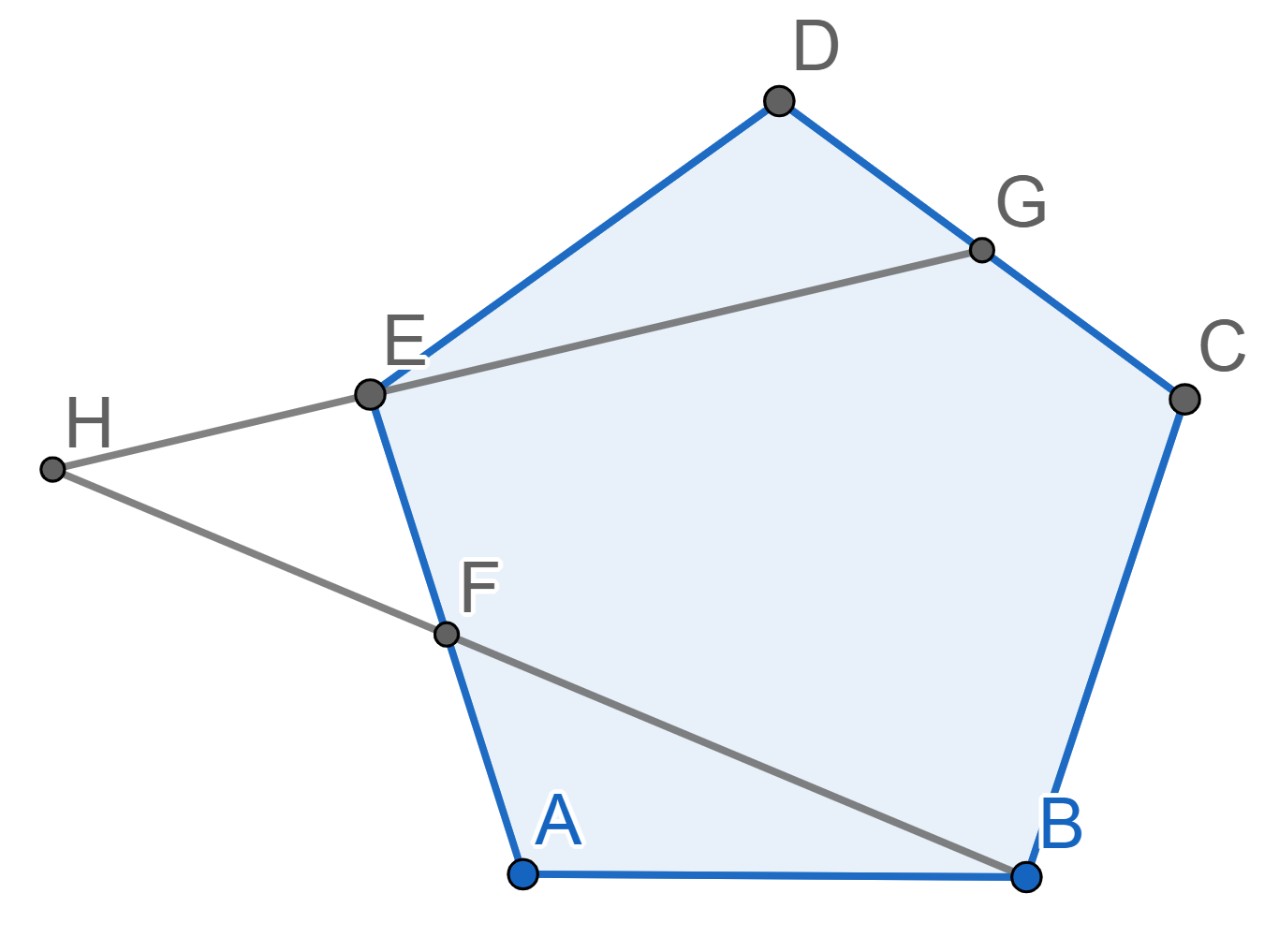
Let \(ABCDE\) be a regular pentagon. The point \(G\) is the midpoint of \(CD\), the point \(F\) is the midpoint of \(AE\). The lines \(EG\) and \(BF\) intersect at the point \(H\). Find the angle \(EHF\).
I have three positive integers. When you add them together, you get \(15\). When you multiply the three numbers together, you get \(120\).
What are the three numbers?
If a magician puts \(1\) dove into his hat, he pulls out \(2\) rabbits and \(2\) flowers from it. If the magician puts \(1\) rabbit in, he pulls out \(2\) flowers and \(2\) doves. If he puts \(1\) flower in, he pulls out \(1\) rabbit and \(3\) doves. The magician starts with \(1\) rabbit. Could he end up with the same number of rabbits, doves, and flowers after performing his hat trick several times?
In the other room there are two doors. The statements on them say:
There is treasure behind at least one of the doors.
There is treasure behind the first door.
Your guide says: The first sign is true if there is treasure behind the first door, otherwise it is false. The second sign is false if there is treasure behind the second door, otherwise it is true. What would you do?
For any real number \(x\), the absolute value of \(x\), written \(\left| x \right|\), is defined to be \(x\) if \(x>0\) and \(-x\) if \(x \leq 0\). What are \(\left| 3 \right|\), \(\left| -4.3 \right|\) and \(\left| 0 \right|\)?
Let \(x\) and \(y\) be real numbers. Prove that \(x \leq \left| x \right|\) and \(0 \leq \left| x \right|\). Then prove that the following inequality holds \(\left| x+y \right| \leq \left| x \right|+\left| y \right|\).