Problems
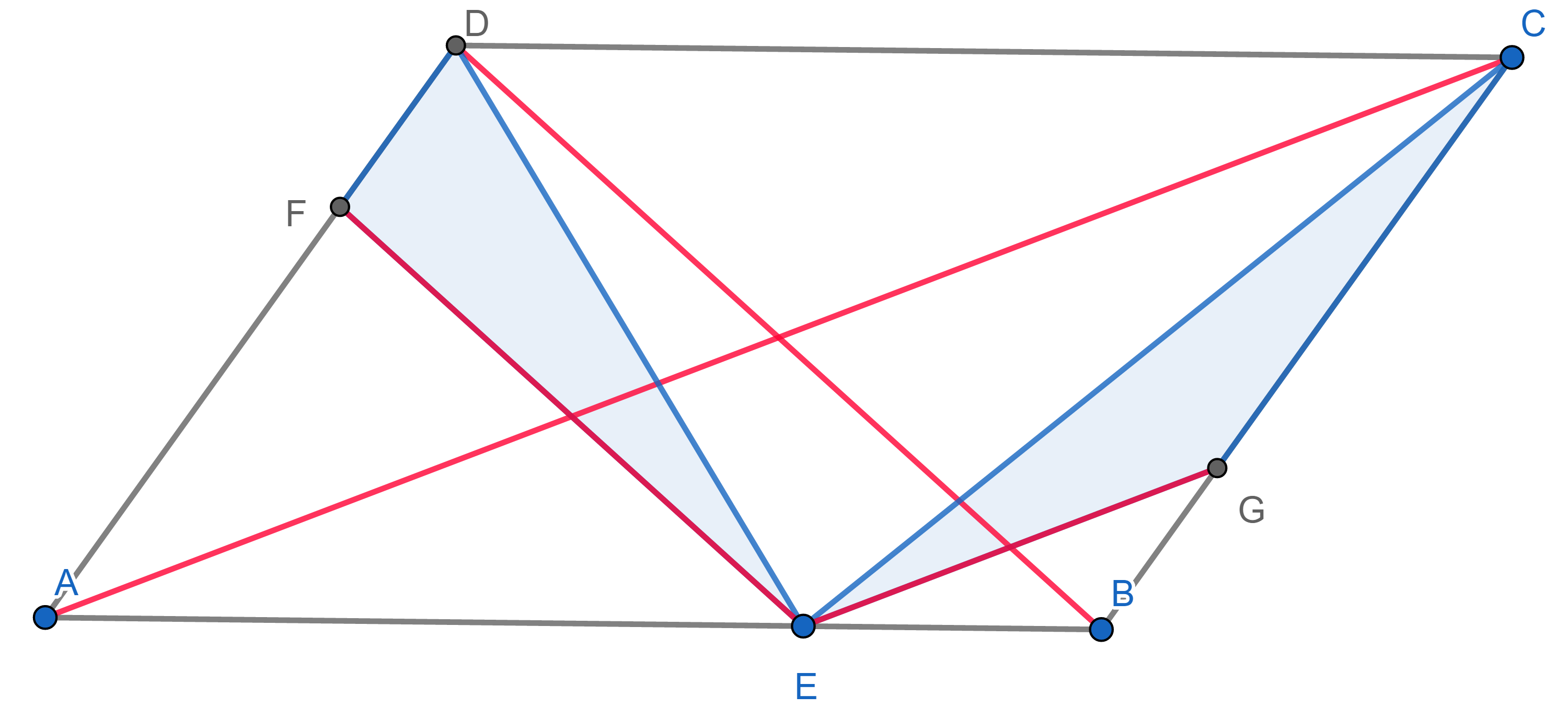
Let \(ABCD\) be a parallelogram. The segment \(EF\) is parallel to the diagonal \(BD\), and the segment \(EG\) is parallel to the diagonal \(AC\). Show that the areas of the triangles \(\triangle EFD\) and \(\triangle EGC\) are equal.
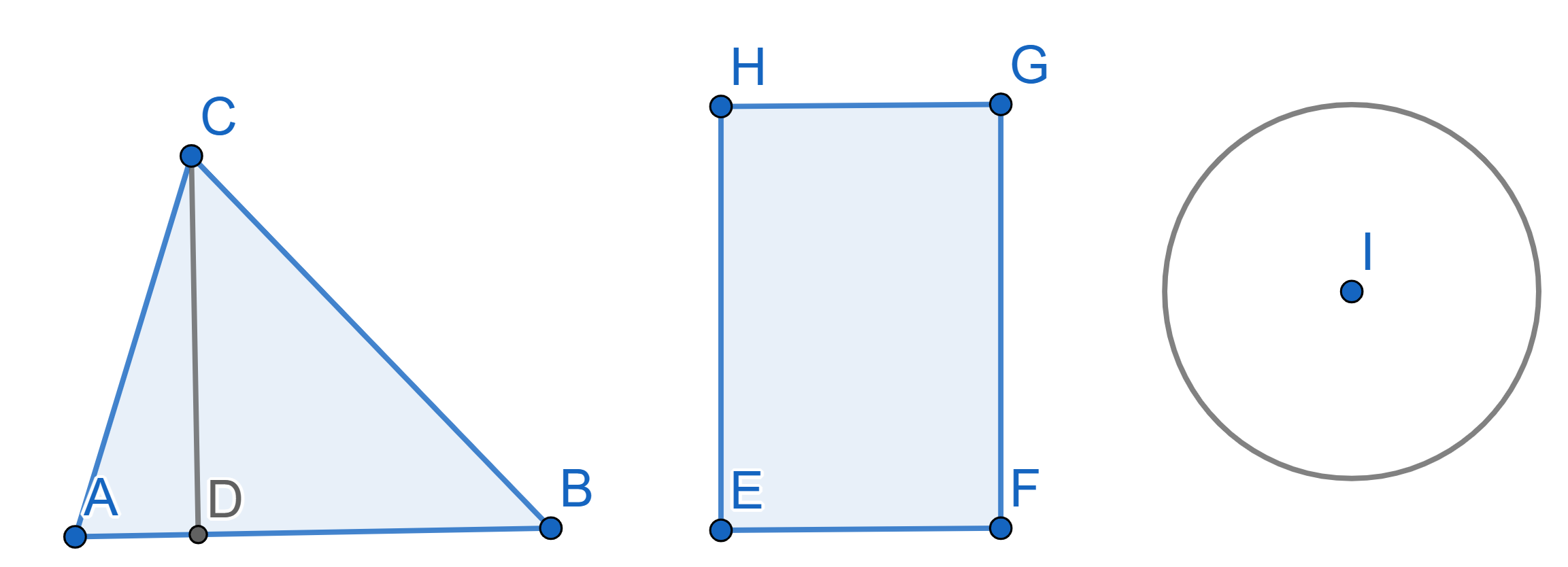
Today we will solve some problems about finding areas of geometric figures. All you need to know in order to solve every problem in this set is: to calculate the area of a triangle we multiply the length of a side by the length of a height to that side and divide by \(2\), namely:\(\frac12 AB \times CD\), as for rectangle we just multiply two adjacent sides (\(EF \times GF\)), and when we have a circle we calculate the area by \(\pi r^2\), where \(r\) is the radius of the circle.
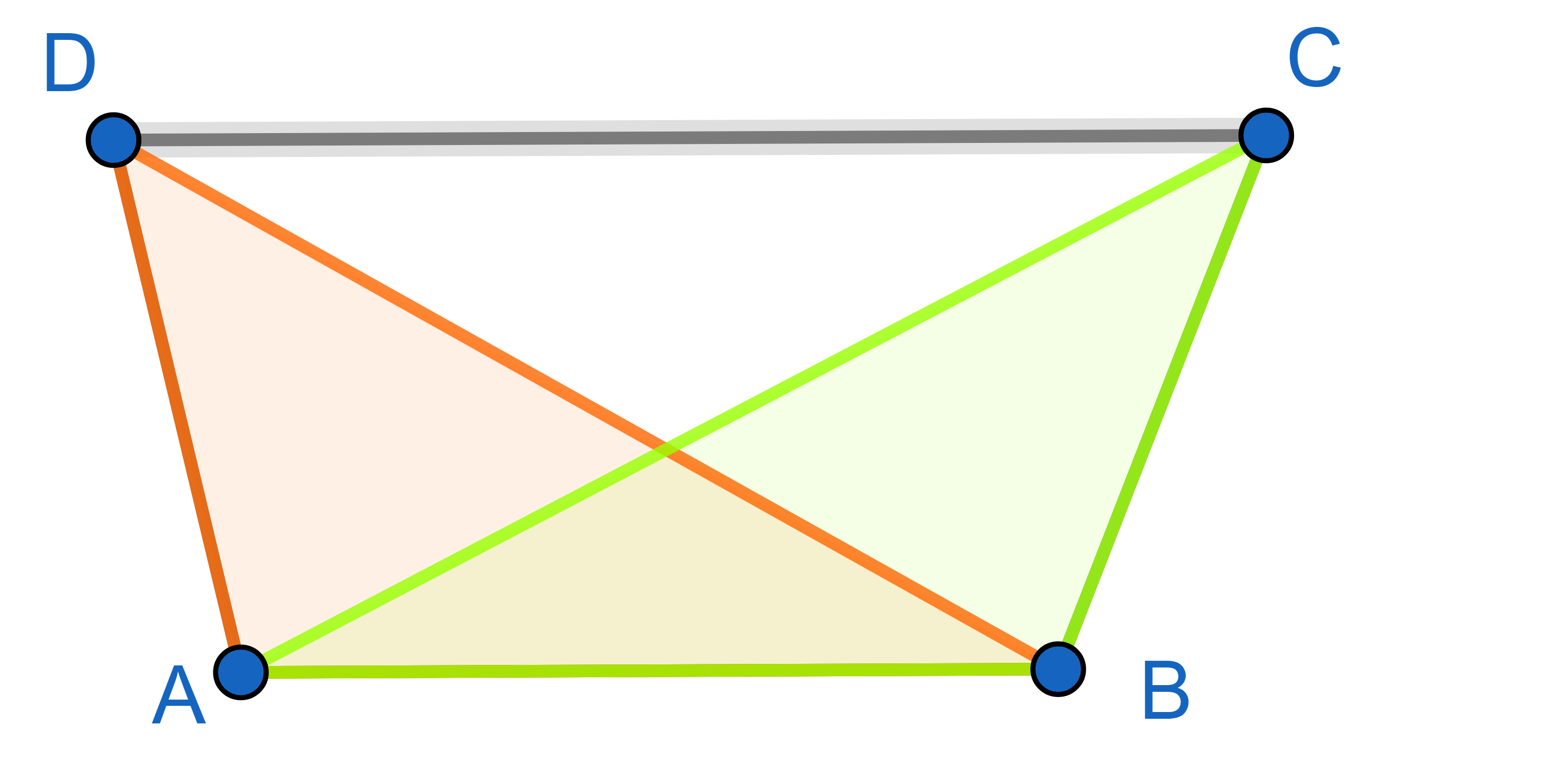
In a trapezium \(ABCD\), the side \(AB\) is parallel to the side \(CD\). Prove that the areas of triangles \(\triangle ABC\) and \(\triangle ABD\) are equal.
On the left there is a circle inscribed in a square with side \(1\). On the right there are \(16\) smaller, identical circles, which all together fit inside a square of side \(1\). Which area is greater, the yellow or the blue one?

A circle is inscribed in a square, and another square is inscribed in the circle. Which area is larger, the blue or the orange one?

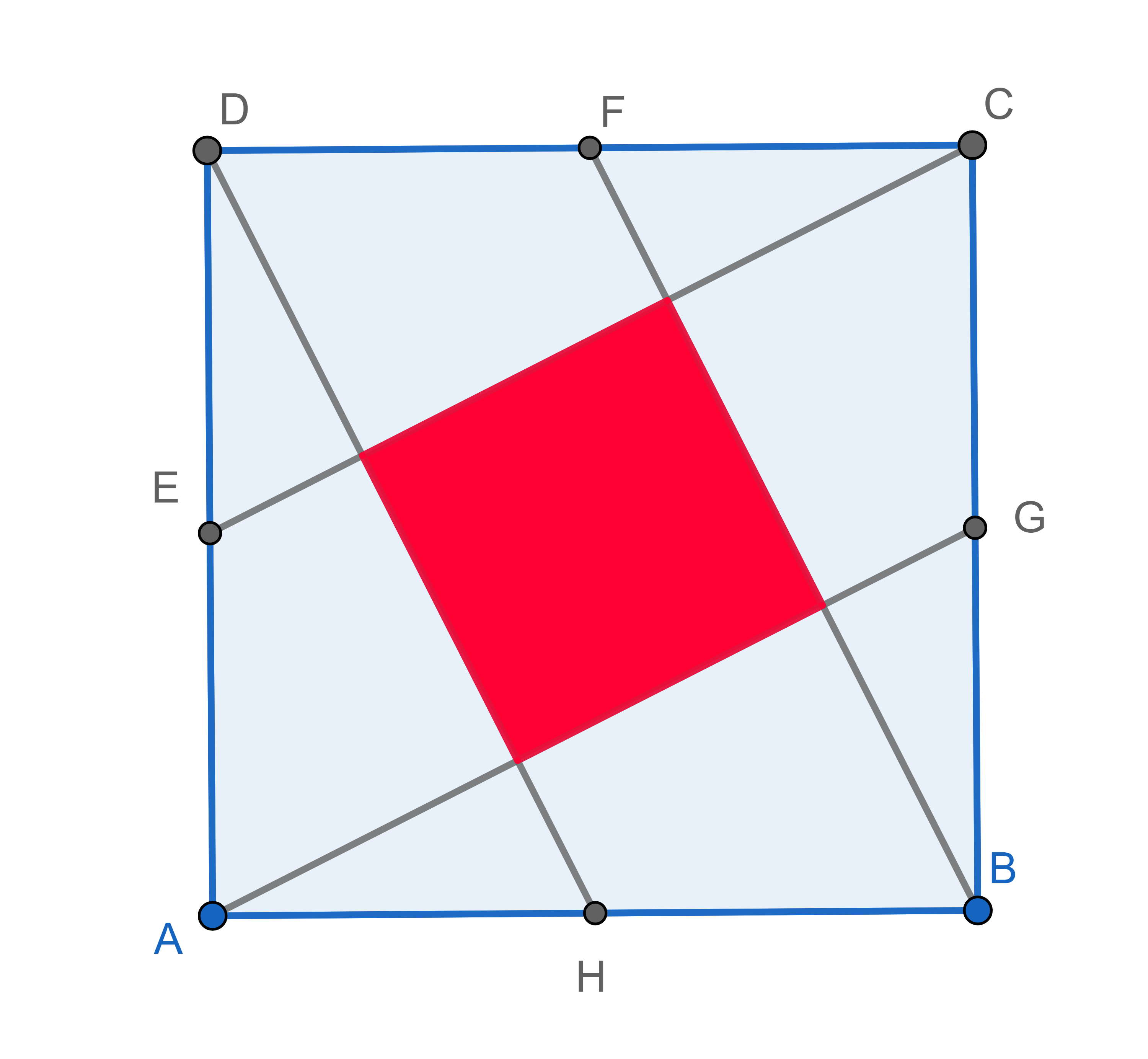
In a square, the midpoints of its sides were marked and connected to the vertices of the square. There is another square formed in the centre. The side length of the large square is \(10\). Find the area of the smaller square. (That is, the red one)
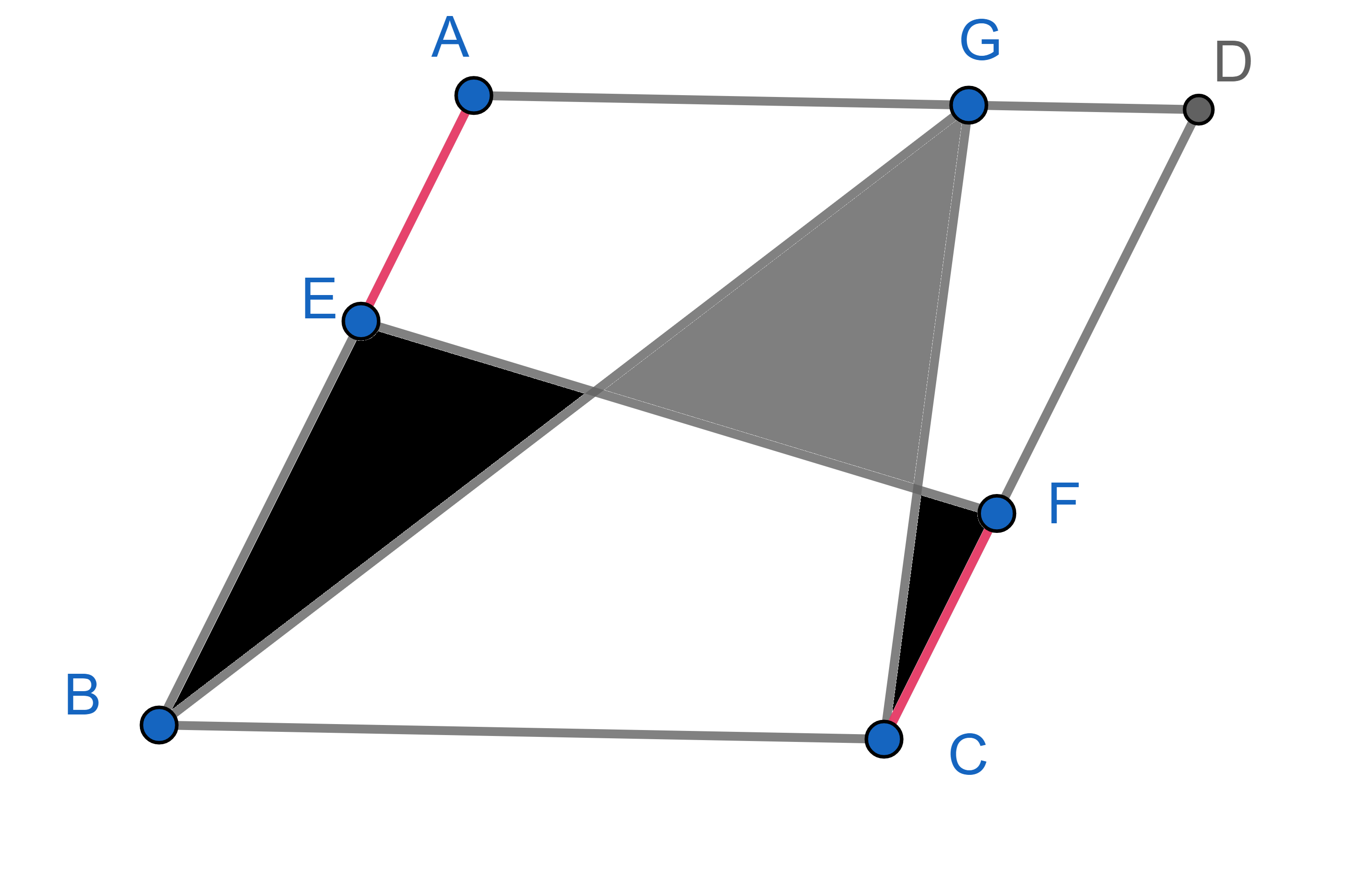
In a parallelogram \(ABCD\), point \(E\) belongs to the side \(AB\), point \(F\) belongs to the side \(CD\) and point \(G\) belongs to the side \(AD\). We know that the marked red segments \(AE\) and \(CF\) have equal lengths. Prove that the total grey area is equal to the total black area.
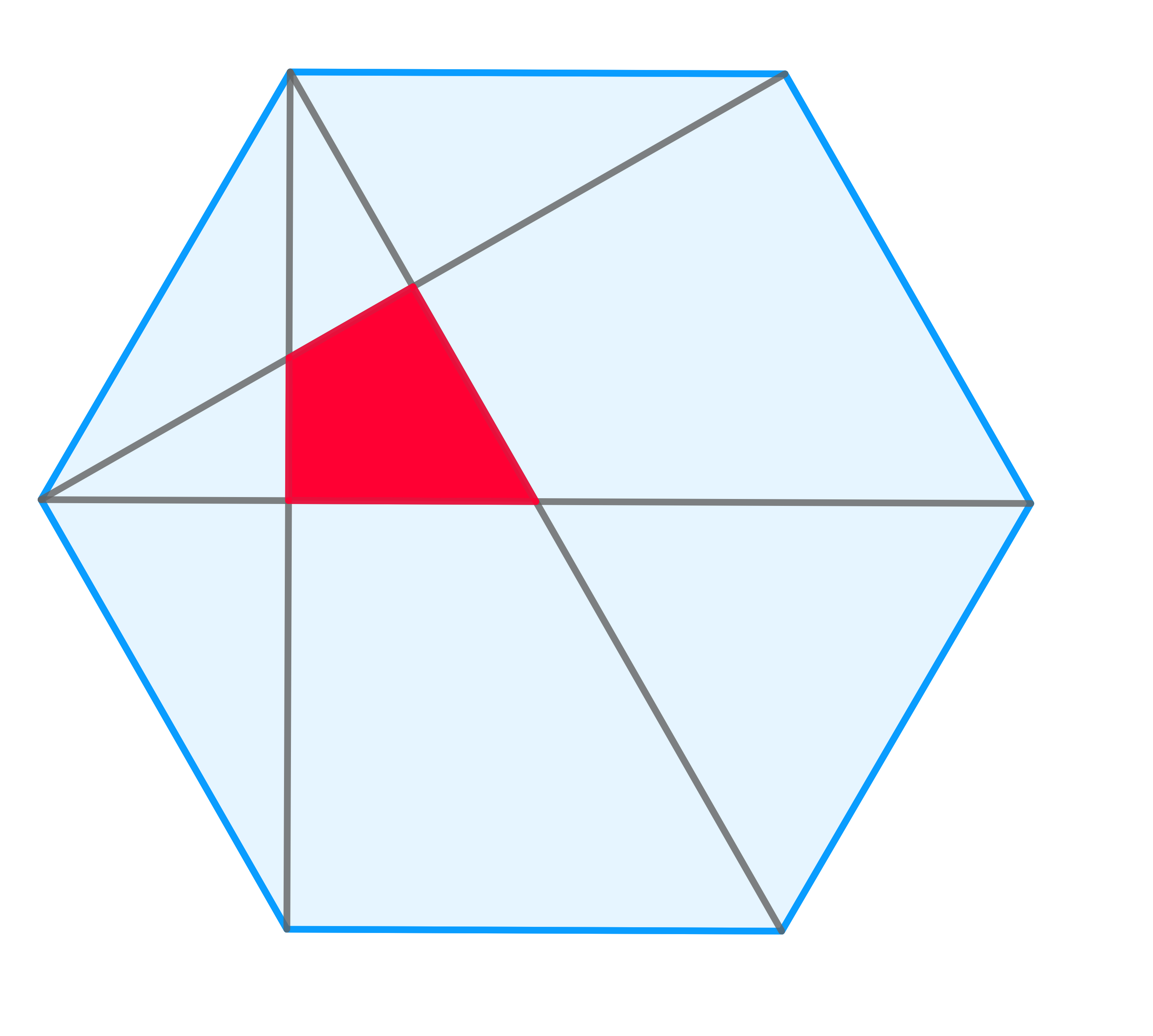
In a regular hexagon of area \(72\), some diagonals were drawn. Find the area of the red region.
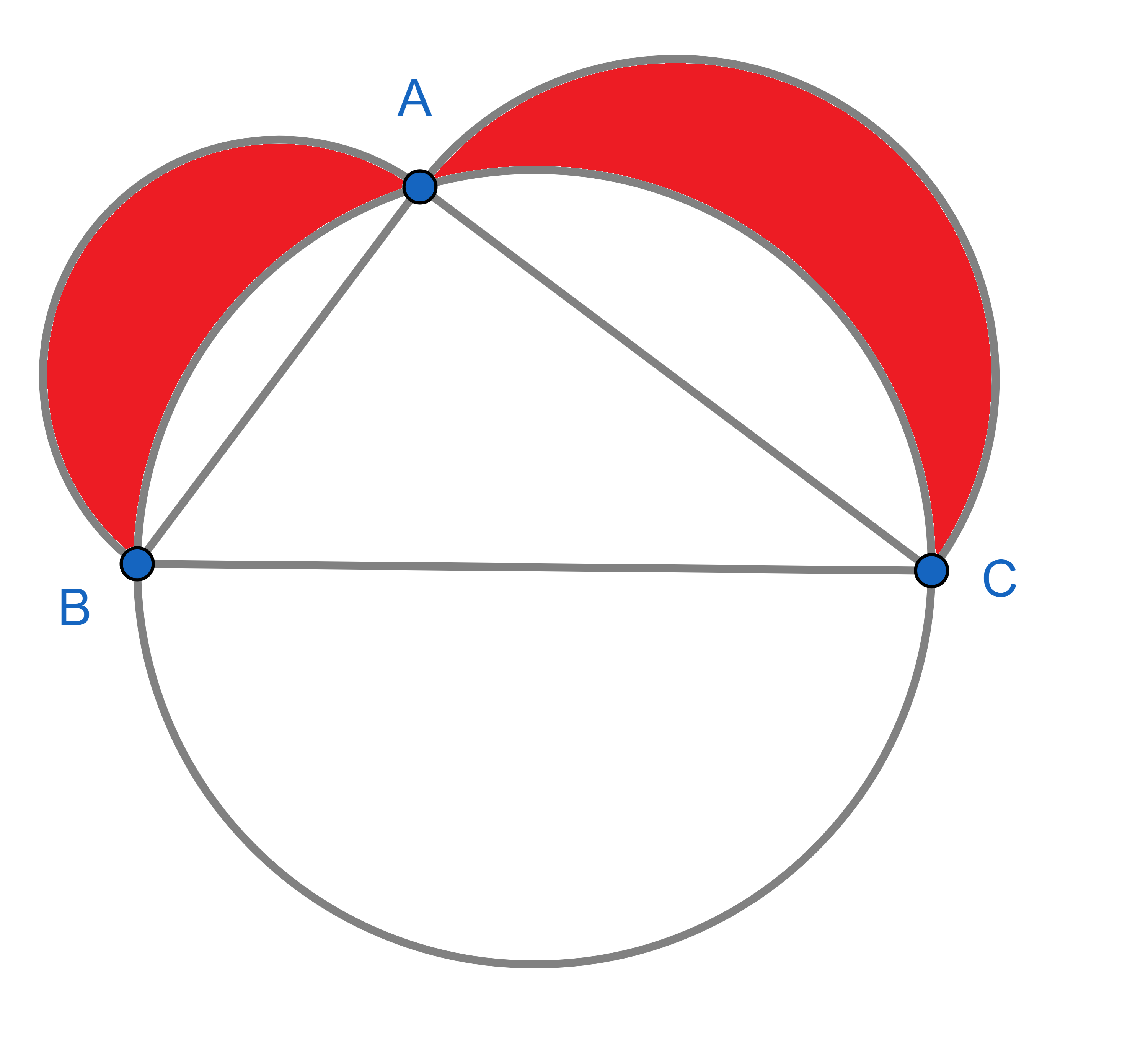
We have a triangle \(\triangle ABC\) with side lengths \(|AB|=3\), \(|AC|=4\) and angle \(\angle BAC=90^{\circ}\). A circle is drawn with side \(BC\) as diameter, and two semicircles are drawn with sides \(AB\) and \(AC\) as diameters. Find the area of the red part.
Today we will be solving problems using the Pigeonhole Principle. What is it? Simply put, suppose we are asked to put pigeons inside pigeonholes, but we have more pigeons that pigeonholes. No matter how we try to do it, there will be a pigeonhole with at least two pigeons. For example, consider the following picture, where we have \(10\) pigeons but only \(9\) pigeonholes:

No matter how hard we try to arrange the pigeons, it will be
impossible to fit at most \(1\) pigeon
in each pigeonhole! Here is a way to see why: suppose that in each
pigeonhole there was at most \(1\)
pigeon. Since we have \(9\)
pigeonholes, this means we have at most \(1\times 9=9\) pigeons in total, but this is
can’t be true, because we started with \(10\) pigeons!
By pigeonhole we can mean any container, and by pigeon we can mean any
object that we want to place inside the containers. This is a simple but
very powerful idea, and today we will learn how to use it to solve some
difficult problems! Let’s start by seeing a simple example. Can you see
what the pigeonholes and the pigeons should be?