Problems
Imagine you have now a general finite number of new guests arriving to the full hotel. What do you do?
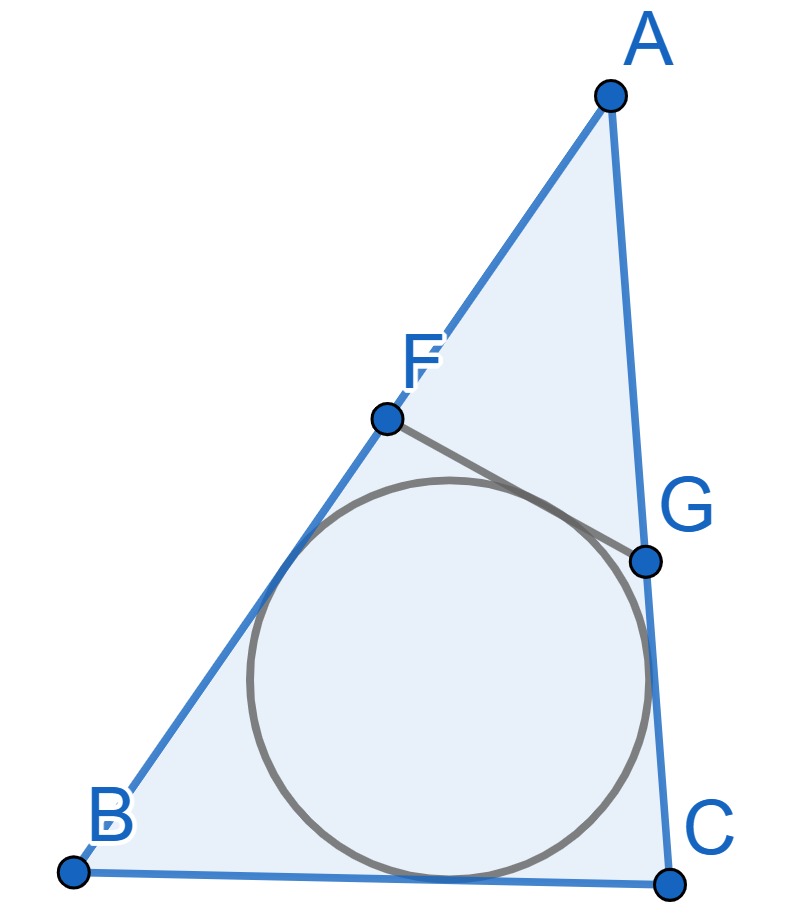
A circle is inscribed into the triangle \(ABC\) with sides \(BC=6, AC=10\) and \(AB= 12\). A line tangent to the circle intersects two longer sides of the triangle \(AB\) and \(AC\) at the points \(F\) and \(G\) respectively. Find the perimeter of the triangle \(AFG\).
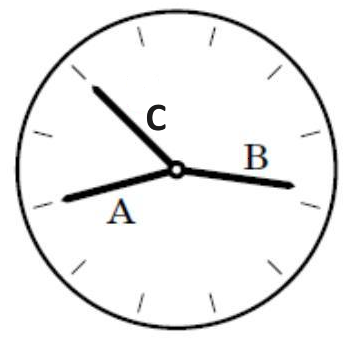
Liam saw an unusual clock in the museum: the clock had no digits, and it’s not clear how the clock should be rotated. That is, we know that \(1\) is the next digit clockwise from \(12\), \(2\) is the next digit clockwise from \(1\), and so on. Moreover all the arrows (hour, minute, and second) have the same length, so it’s not clear which is which. What time does the clock show?
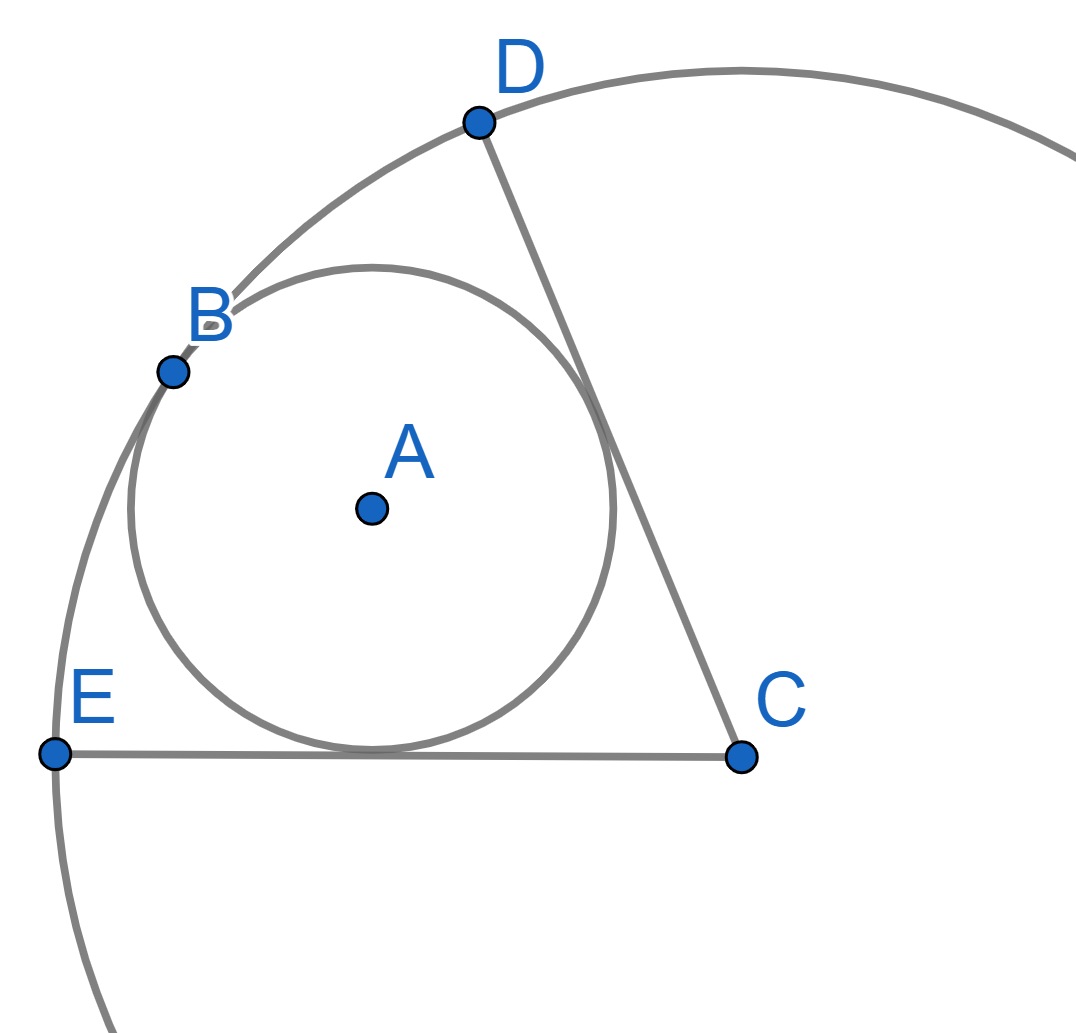
Two circles are tangent to each other and the smaller circle with the center \(A\) is located inside the larger circle with the center \(C\). The radii \(CD\) and \(CE\) are tangent to the smaller circle and the angle \(\angle DCE = 60^{\circ}\). Find the ratio of the radii of the circles.
For positive real numbers \(a,b,c\) prove the inequality: \[(a^2b + b^2c + c^2a)(ab^2 + bc^2 + ca^2)\geq 9a^2b^2c^2.\]
On a \(10\times 10\) board, a bacterium sits in one of the cells. In one move, the bacterium shifts to a cell adjacent to the side (i.e. not diagonal) and divides into two bacteria (both remain in the same new cell). Then, again, one of the bacteria sitting on the board shifts to a new adjacent cell, either horizontally or vertically, and divides into two, and so on. Is it possible for there to be an equal number of bacteria in all cells after several such moves?
Let \(p\) and \(q\) be two prime numbers such that \(q = p + 2\). Prove that \(p^q + q^p\) is divisible by \(p + q\).
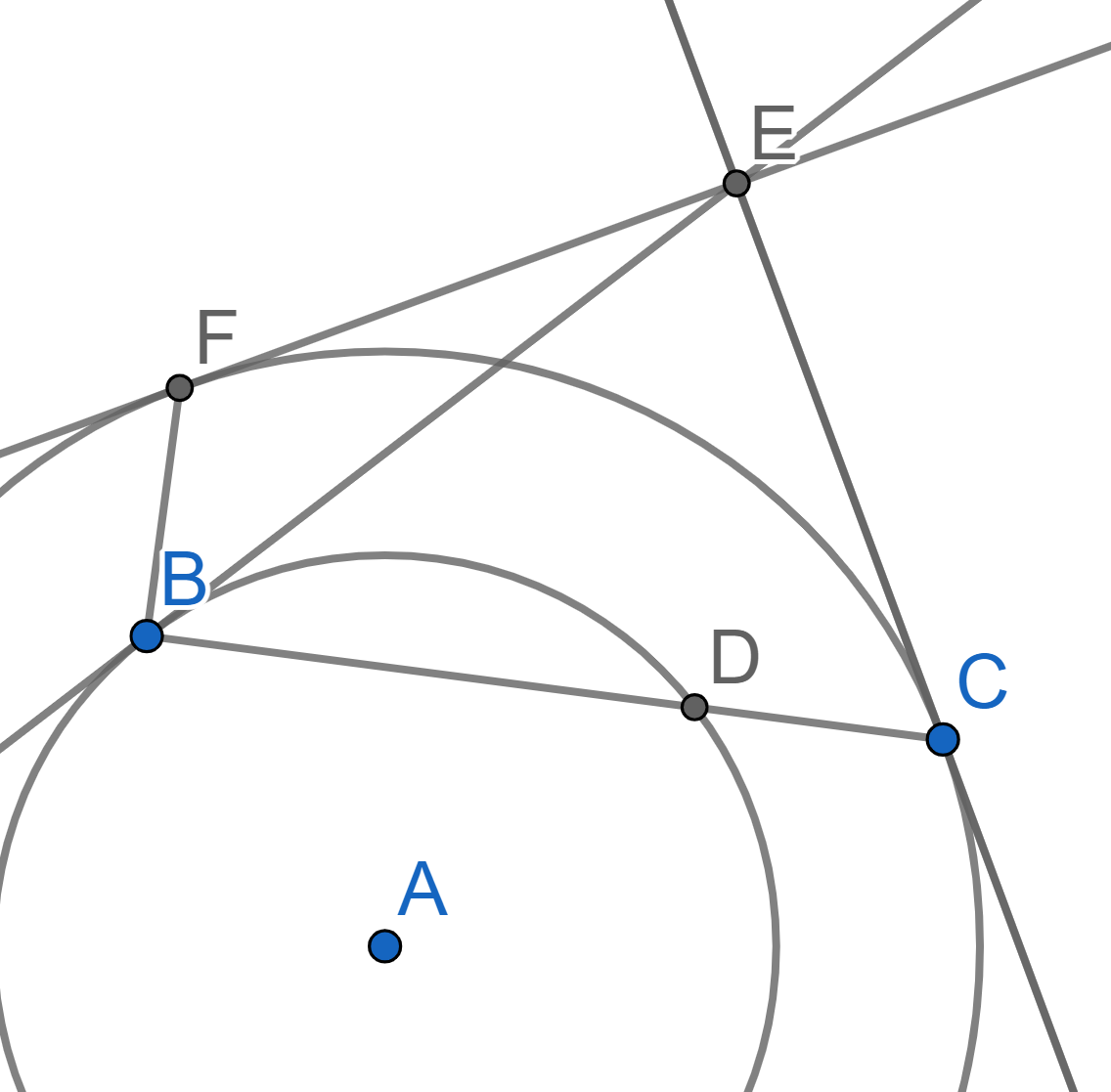
Let \(C_1\) and \(C_2\) be two concentric circles with \(C_1\) inside \(C_2\) and the center \(A\). Let \(B\) and \(D\) be two points on \(C_1\) that are not diametrically opposite. Extend the segment \(BD\) past \(D\) until it meets the circle \(C_2\) in \(C\). The tangent to \(C_2\) at \(C\) and the tangent to \(C_1\) at \(B\) meet in a point \(E\). Draw from \(E\) the second tangent to \(C_2\) which meets \(C_2\) at the point \(F\). Show that \(BE\) bisects angle \(\angle FBC\).
Due to a mistake in the bakery, a cake that was supposed to be shaped as two concentric pieces (like on the right diagram below) came out like the left diagram below. Find the smallest number of pieces the cake should be cut into in order to rearrange the pieces into the cake on the right side of the picture.
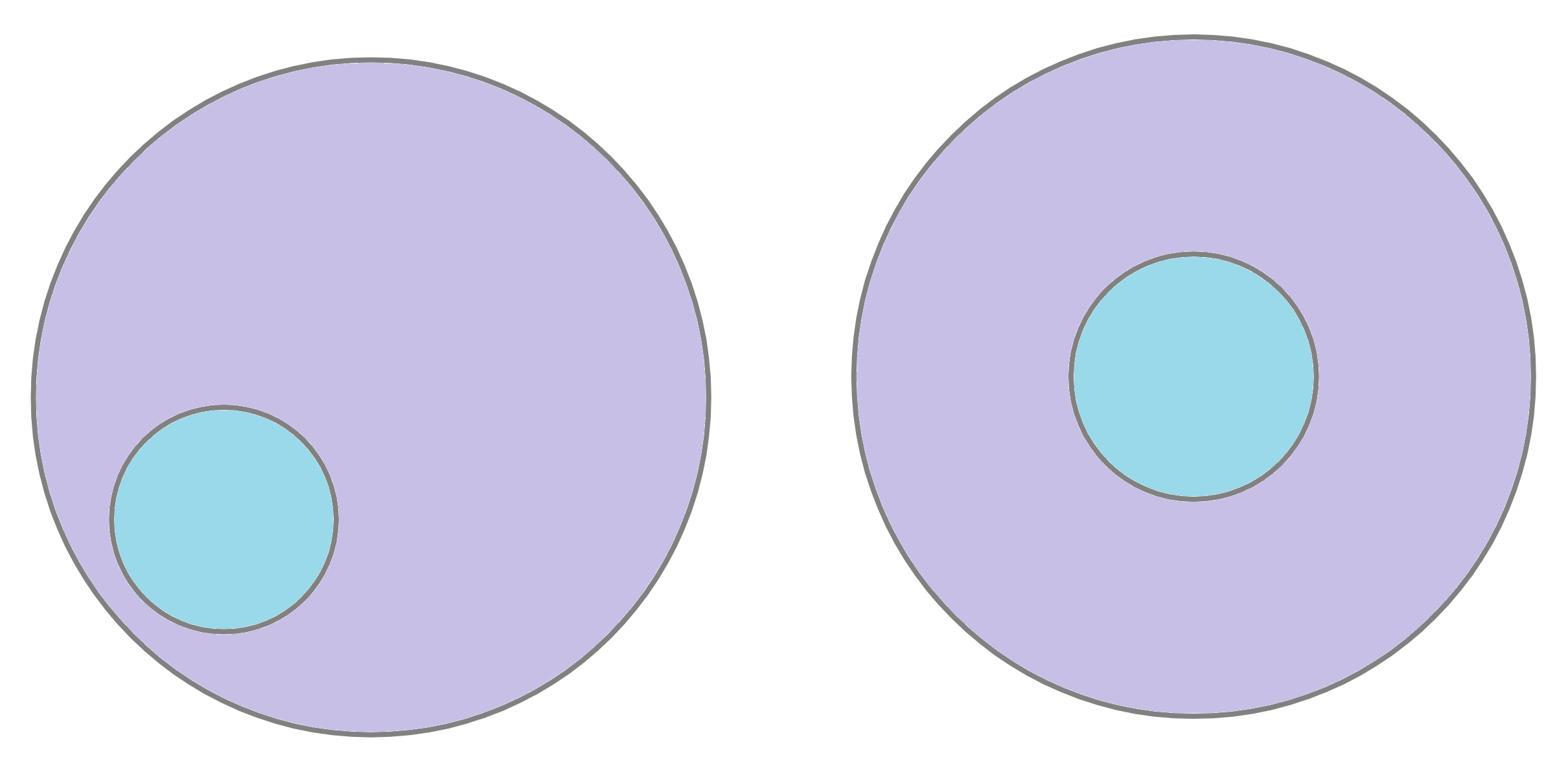
Note that the cake is \(\textit{not}\) tiered like a wedding cake, but is shaped like a cylinder with a flat top. Curved cuts are allowed.
Katie and Charlotte had \(4\) sheets of paper. They cut some of the sheets into \(4\) pieces. They then cut some of the newly obtained papersheets also into \(4\) pieces. They did this several more times, cutting a piece of paper into \(4\). In the end they counted the number of sheets. Could this number be \(2024\)?