Problems

Certain geometric objects nicely blend when they happen to be together in a problem. One possible example of such a pair of objects is a circle and an inscribed angle.
We will be using the following statements in the examples and problems:
1. The supplementary angles (angles “hugging" a straight line) add up to \(180^{\circ}\).
2. The sum of all internal angles of a triangle is also \(180^{\circ}\).

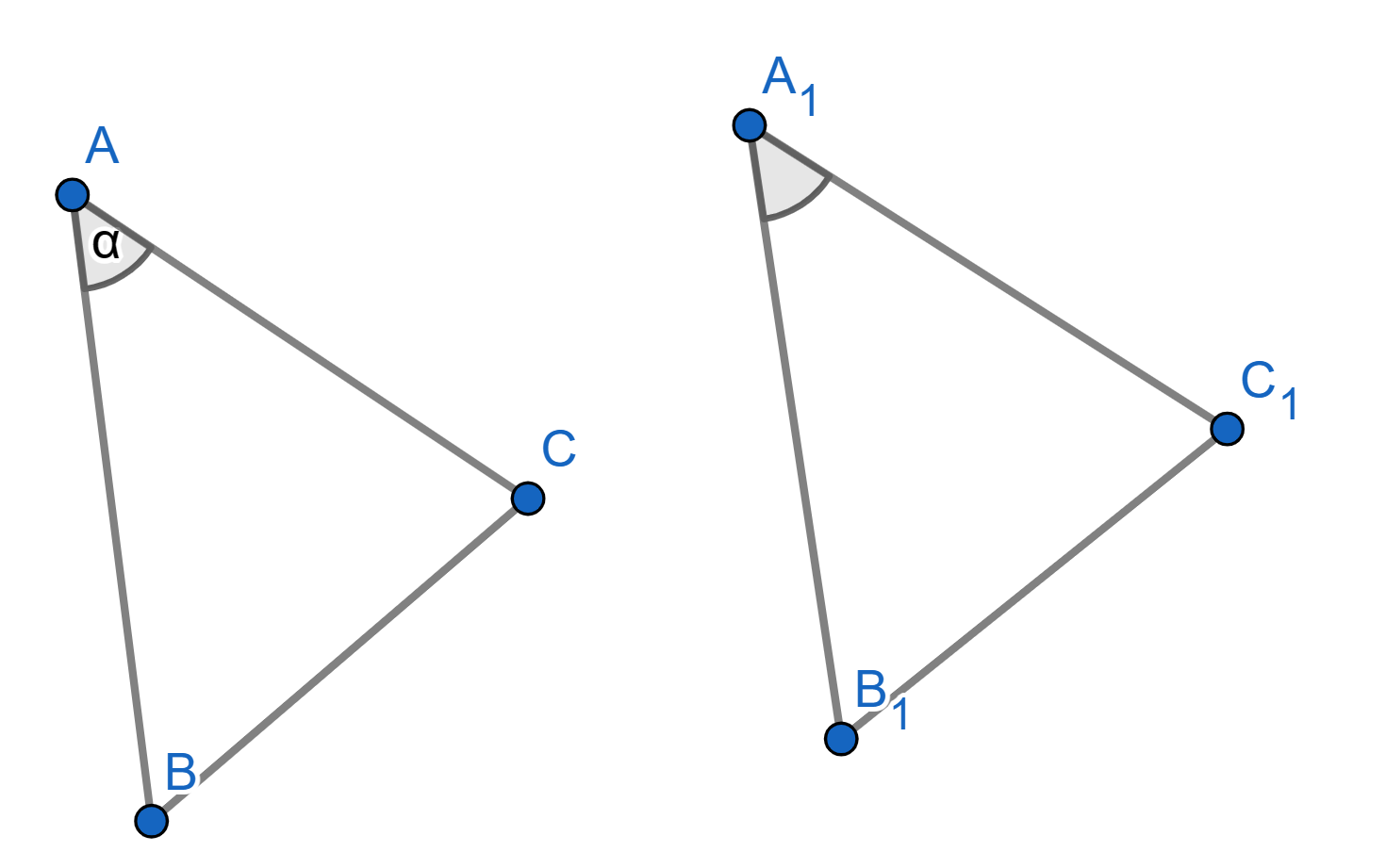
3. Two triangles are said to be “congruent" if ALL their corresponding sides and angles are equal.
We recommend solving the problems in this sheet in the order of appearance, as some problems use statements from previous problems as a step in the solution. Specifically, the inscribed angle theorem (problem 2) is required to solve every other problem that comes after it.

Let \(ABC\) and \(A_1B_1C_1\) be two triangles with the following properties: \(AB = A_1B_1\), \(AC = A_1C_1\), and angles \(\angle BAC = \angle B_1A_1C_1\). Then the triangles \(ABC\) and \(A_1B_1C_1\) are congruent. This is usually known as the “side-angle-side" criterion for congruence.

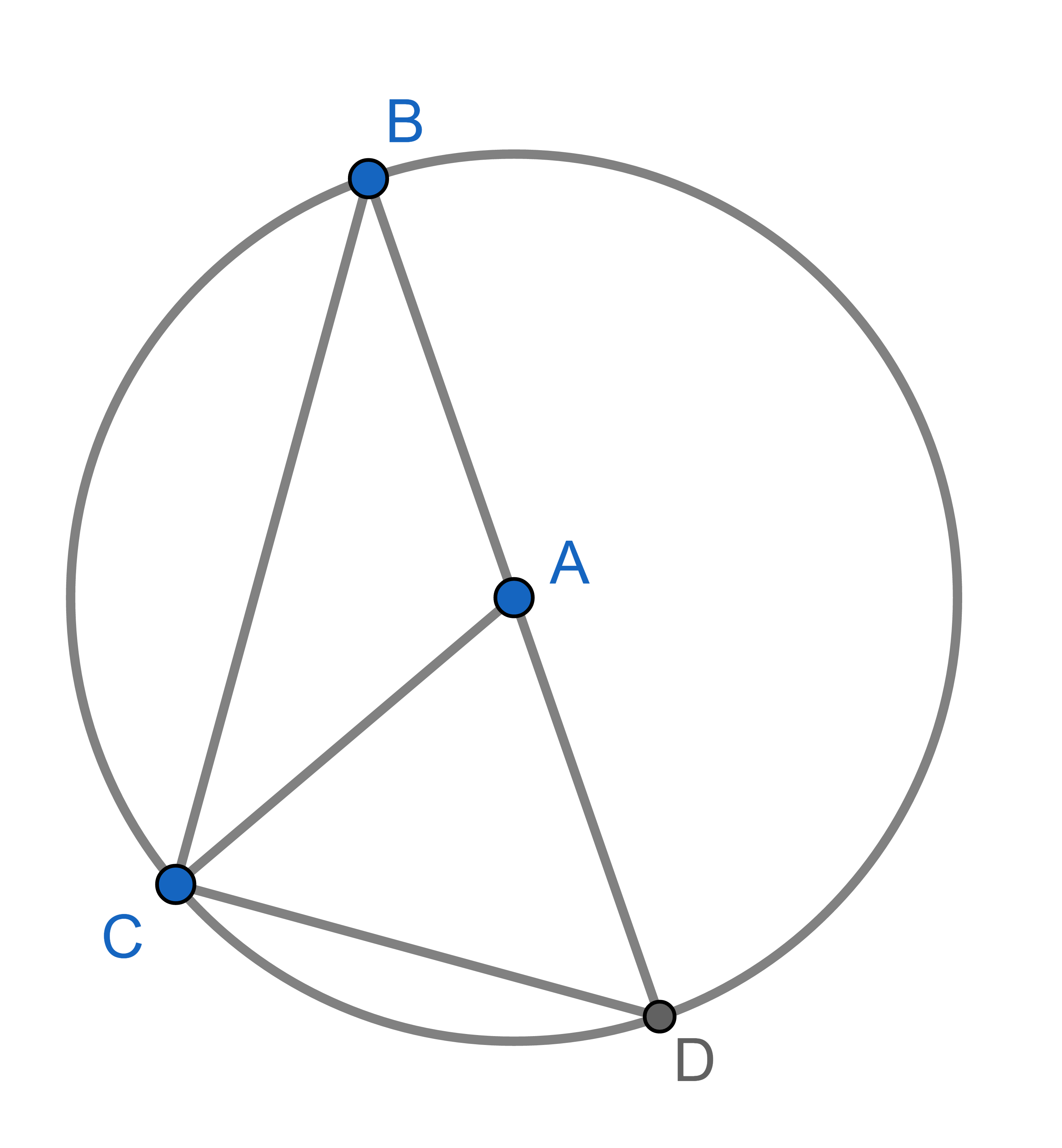
In the triangle \(\triangle ABC\) the sides \(AC\) and \(BC\) are equal. Prove that the angles \(\angle CAB\) and \(\angle CBA\) are equal.

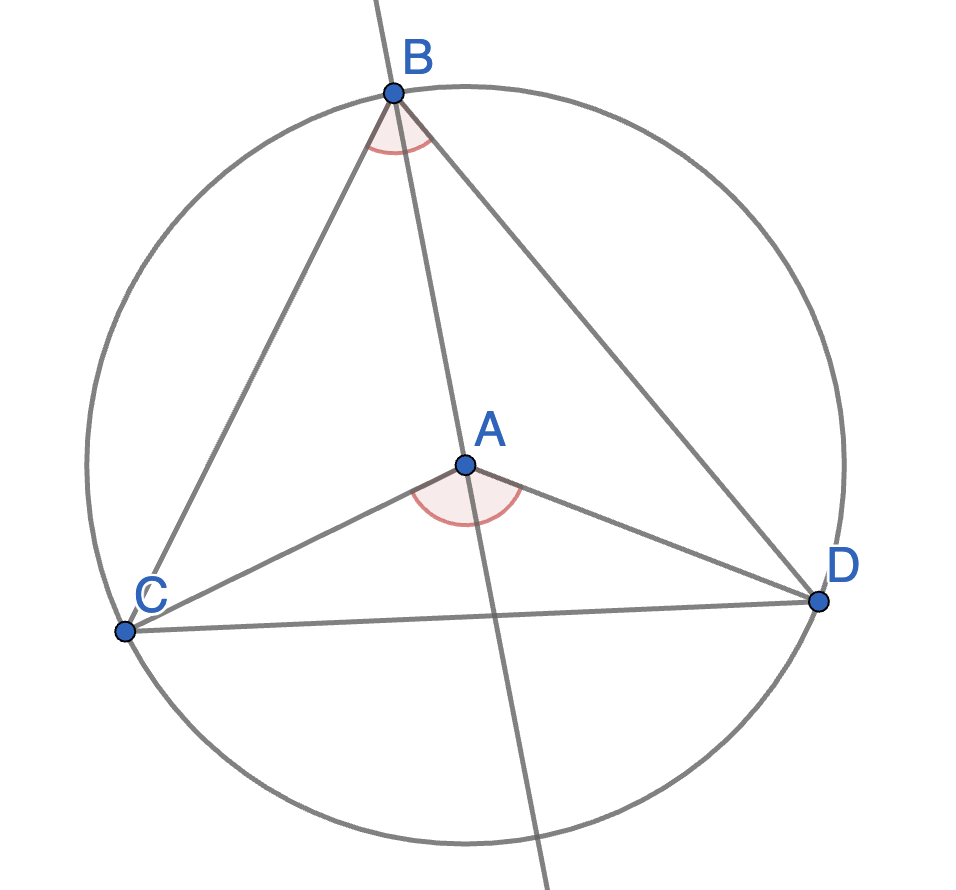
Point \(A\) is the centre of a circle and points \(B,C,D\) lie on that circle. The segment \(BD\) is a diameter of the circle. Show that \(\angle CAD = 2 \angle CBD\). This is a special case of the inscribed angle theorem.

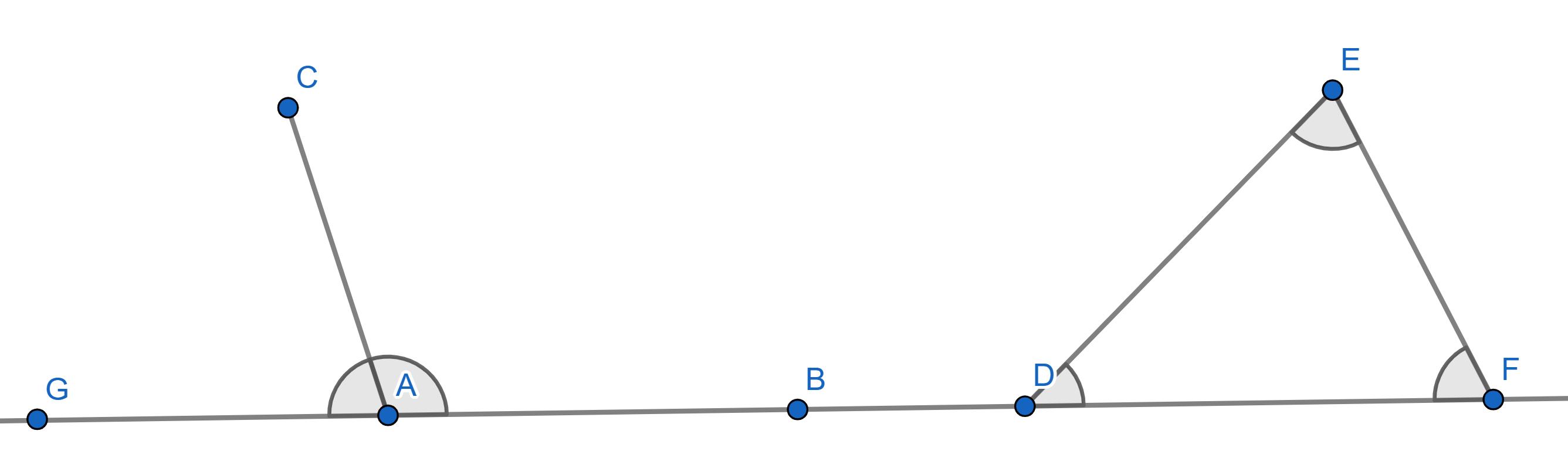
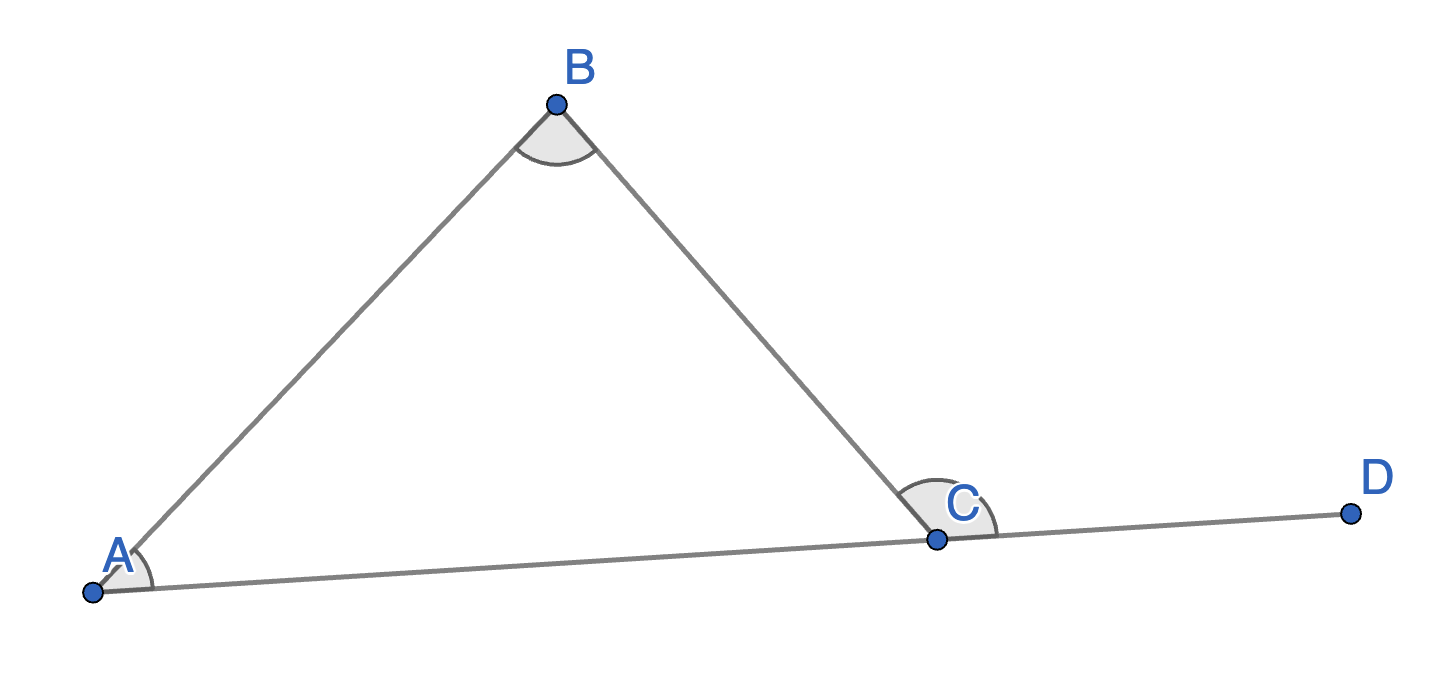
Let \(ABC\) be a triangle with given angles \(\angle BAC\) and \(\angle ABC\). What is the value of the angle \(\angle BCD\) in terms of \(\angle BAC\) and \(\angle ABC\)?

Point \(A\) is the centre of a circle and points \(B,C,D\) lie on that circle. Show that \(\angle CAD = 2 \angle CBD\). This statement is known as the inscribed angle theorem and is used widely in Euclidean geometry.

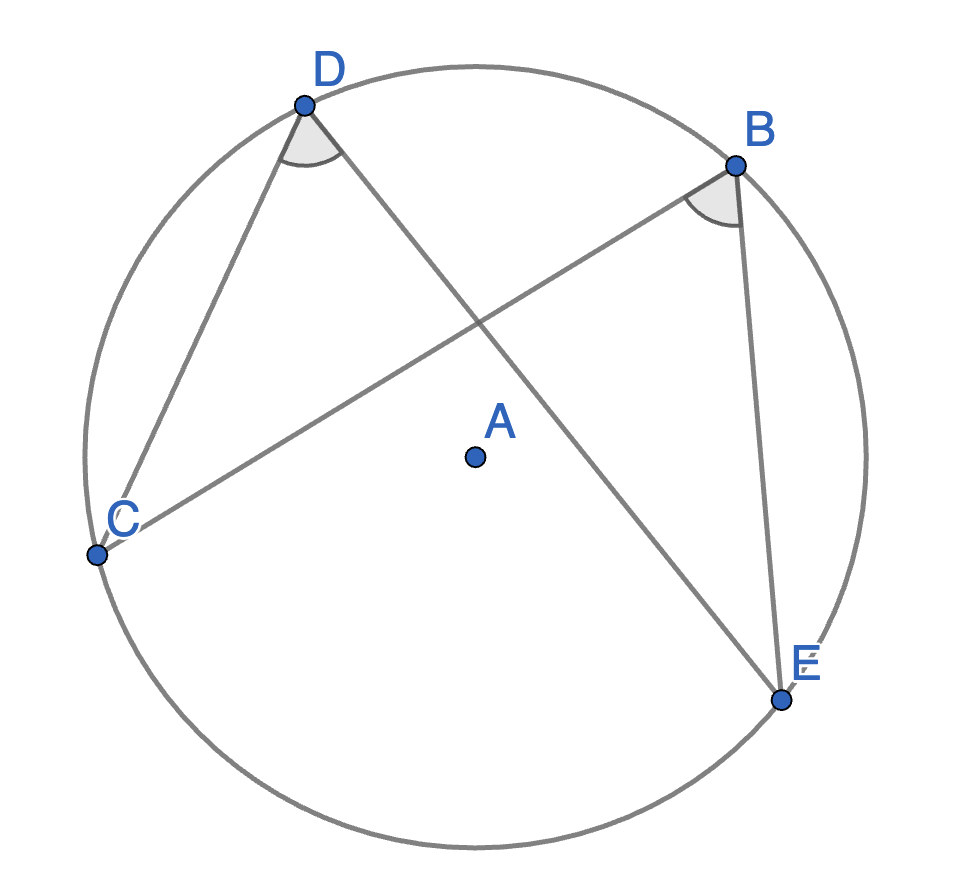
Let \(BCDE\) be a quadrilateral inscribed in a circle with centre \(A\). Show that angles \(\angle CDE\) and \(\angle CBE\) are equal. Also show that angles \(\angle BCD\) and \(\angle BED\) are equal. This says that all angles at the circumference subtended by the same arc are equal.

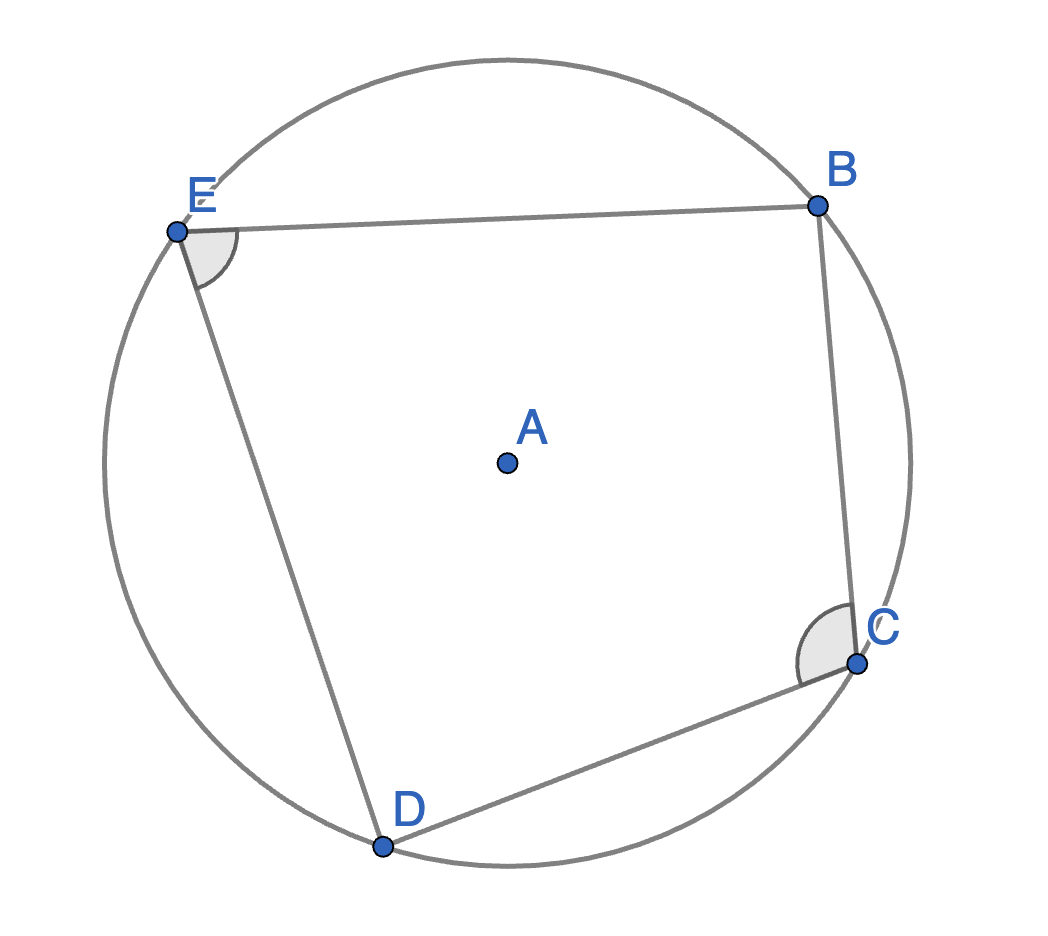
Let \(BCDE\) be an inscribed quadrilateral. Show that \(\angle BCD + \angle BED = 180^{\circ}\).

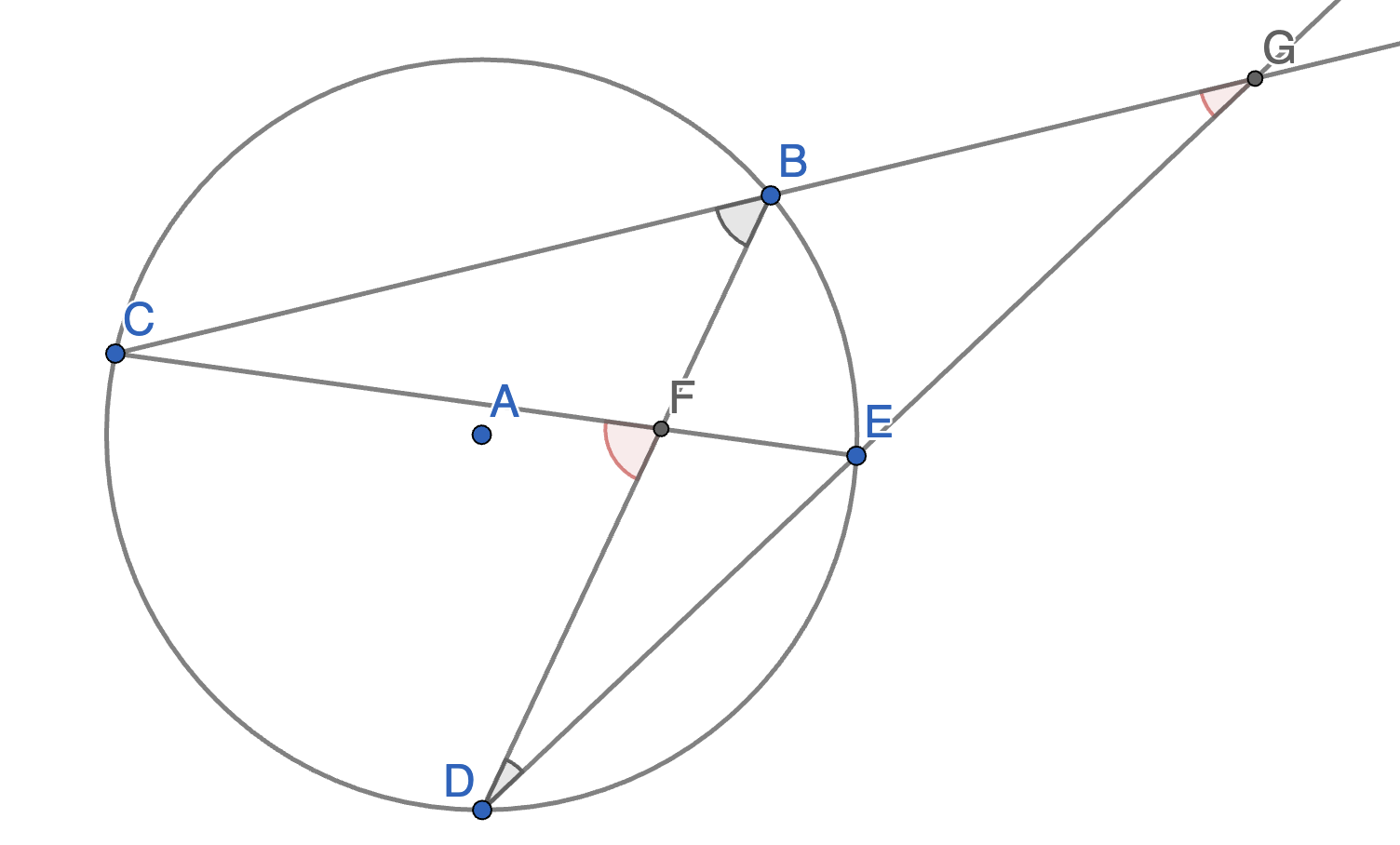
The points \(B\),\(C\),\(D\),\(E\),\(F\) and \(G\) lie on a circle with centre \(A\). The angles \(\angle CBD\) and \(\angle EFG\) are equal. Prove that the segments \(CD\) and \(EG\) have equal lengths.

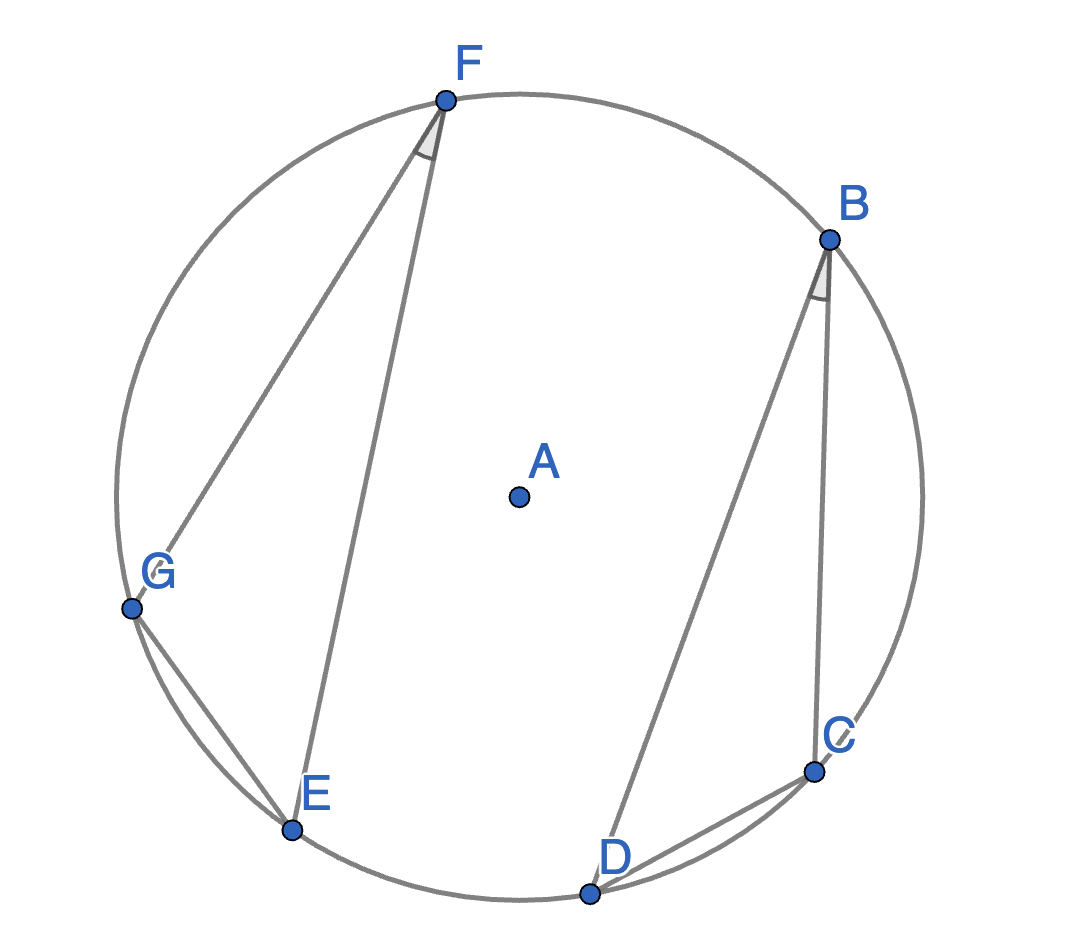
On the diagram below find the value of the angles \(\angle CFD\) and \(\angle CGD\) in terms of angles \(\angle CBD\) and \(\angle BDE\).