Problems
Let \(p\) be a prime number greater than \(3\). Prove that \(p^2-1\) is divisible by \(12\).
In this sheet, we will look at basic counting problems. The fundamental principle is quite simple. If you have two independent choices to make, then the number of options for making both choices is calculated by multiplying the number of options for each choice.
An issue we frequently run into is that of overcounting. This means we count the same thing more than once. In the examples and problems today, you will see various ideas that we can use to correct for overcounting, or for avoiding it.
From the examples above, we see that we often need to pick \(k\) objects from \(n\) objects where the order of the \(k\) objects is ignored. The number of ways to pick them is notated with the special symbol \(\binom{n}{k}\), pronounced "\(n\) choose \(k\)". What’s a formula for \[\binom{n}{k}\]?
By checking which of the following numbers are divisible by \(11\): \[121,\,143,\,286,\,235,\,473,\,798,\,693,\,576,\,748\] can you find and prove a condition that is enough to guarantee a number is divisible by \(11\)?
You meet an alien, who you learn is thinking of a positive integer \(n\). They ask the following three questions.
“Am I the kind who could ask whether \(n\) is divisible by no primes other than \(2\) or \(3\)?"
“Am I the kind who could ask whether the sum of the divisors of \(n\) (including \(1\) and \(n\) themselves) is at least twice \(n\)?"
“Is \(n\) divisible by 3?"
Is this alien a Crick or a Goop?
Today we will solve some problems about finding areas of geometric figures. You only need to know how to calculate the area of a rectangle, a triangle and a circle to be able to solve every problem in this set. Here is a brief description of the area formula for each shape.
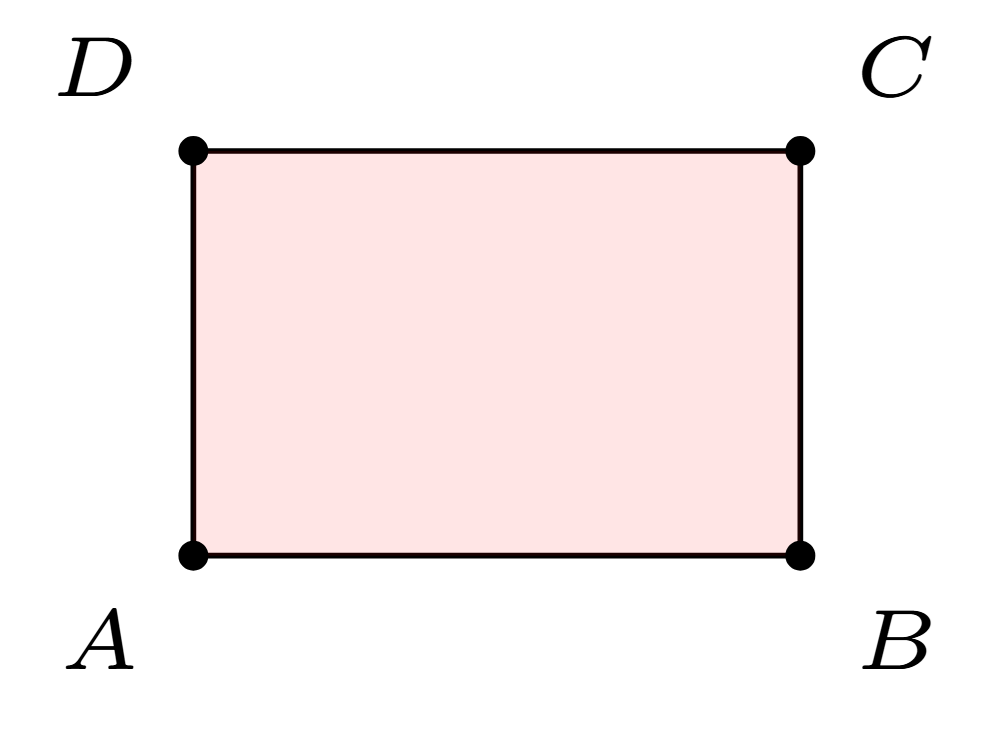
We start with rectangles because they are easy. In the picture below, one way to find the area of the rectangle is to multiple the length of the side \(AB\) by the length of the side \(AD\).
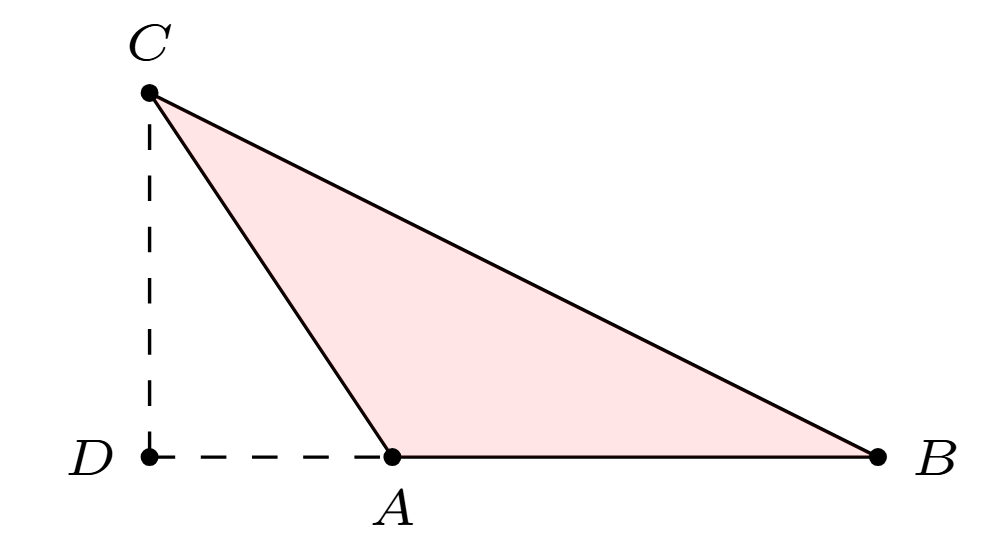
Next we consider the area of a triangle. In general, the area of a triangle is given by \(\frac{1}{2}bh\), where \(b\) is the length of a chosen base and \(h\) is the height (the length of the altitude corresponding to that base). Finding a base and a corresponding altitude is usually straightforward. However, it can be a bit tricky if the altitude lies outside the triangle. See the picture below for one such case. The segment \(AB\) is the base and \(CD\) is the altitude.
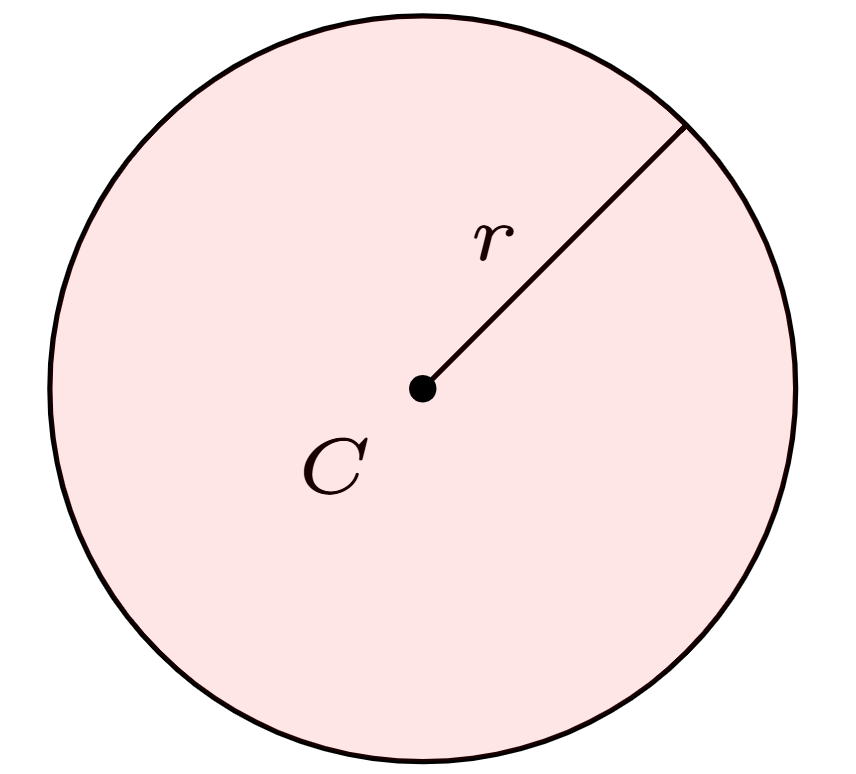
At last, we come to the area of a circle. If a circle has radius \(r\), its area is \(\pi r^2\). A fully rigorous proof requires calculus! The number \(\pi\) is approximately 3.14159 to five decimal points.
Find the mistake in the sequence of equalities: \(-1=(-1)^{\frac{2}{2}}=((-1)^2)^{\frac{1}{2}}=1^{\frac{1}{2}}=1\).
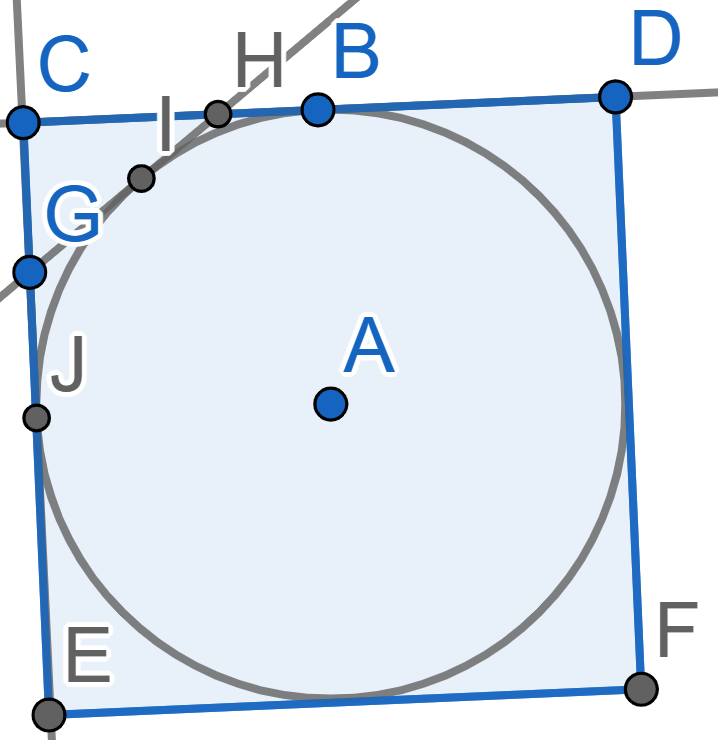
A circle with center \(A\) is inscribed into a square \(CDFE\). A line \(GH\) intersects the sides \(CD\) and \(CE\) of the square and is tangent to the circle at the point \(I\). Find the perimeter of the triangle \(CHG\) (the sum of lengths of all the sides) if the side of the square is \(10\)cm.
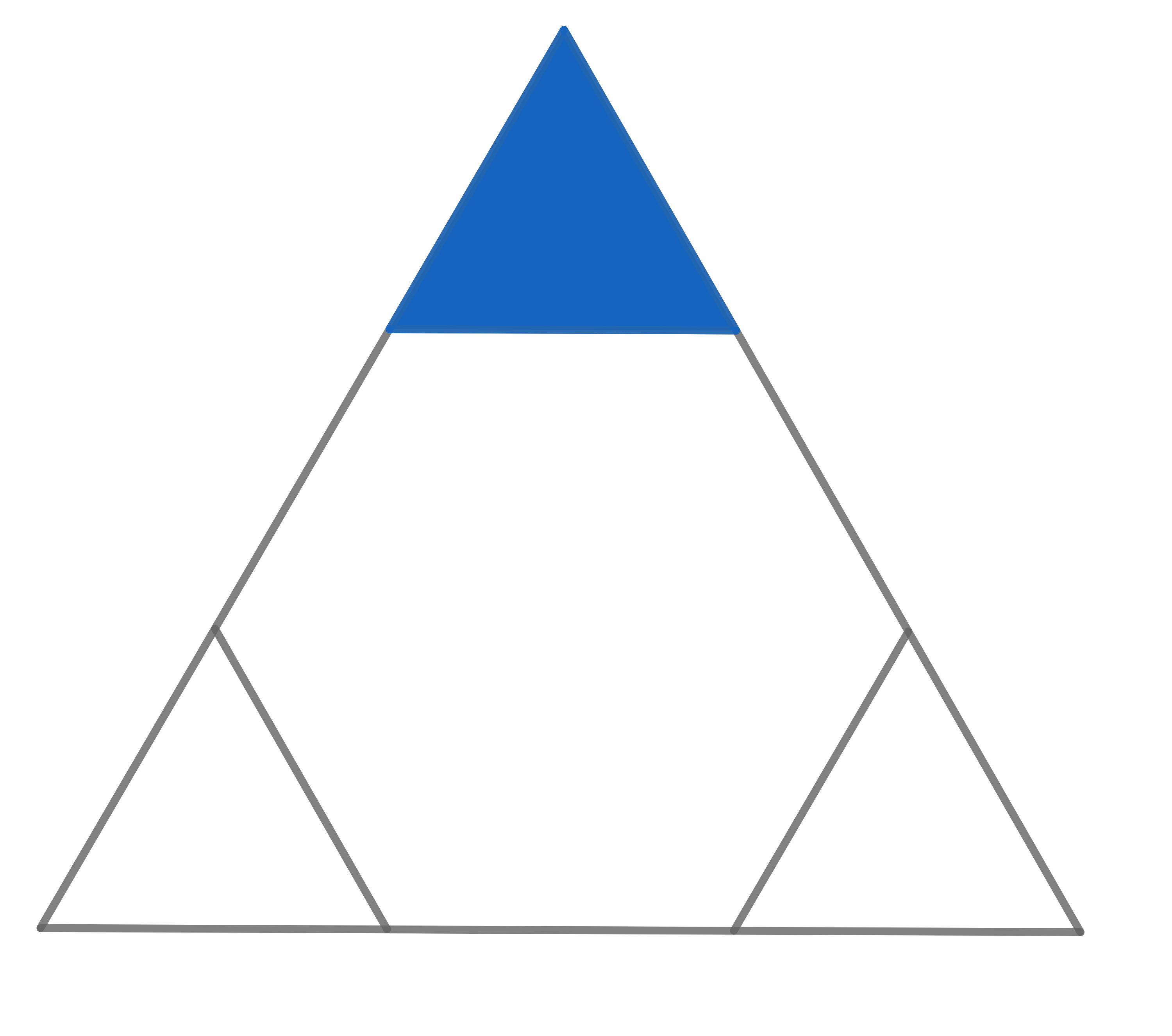
The triangle visible in the picture is equilateral. The hexagon inside is a regular hexagon. If the area of the whole big triangle is \(18\), find the area of the small blue triangle.