Problems

Prove that \(6\) is the maximum possible number of living neighbours a dead cell can have in a still life, and show that this maximum can actually occur.

A spaceship is a pattern that, after a fixed number of generations, looks exactly the same as before, but in a different place. For example, the glider is the pattern shown below: it looks the same every \(4\) generations, and each time it has moved one square diagonally. It turns out this is a speed limit in the game! Show that no pattern can move \(2\) or more squares diagonally after \(4\) generations.

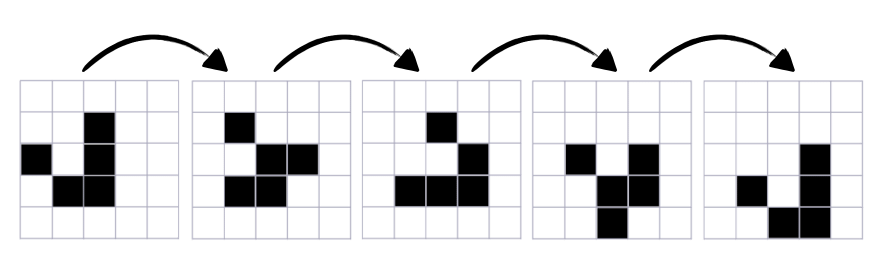
A phoenix is a pattern with the interesting property that all of its alive cells die after each generation, yet the pattern as a whole lives indefinitely. Show that if a phoenix is contained in some rectangle at the start, it can never extend more than one cell past this rectangle (i.e: a phoenix can’t expand forever). Below is a picture of a phoenix with period \(2\):

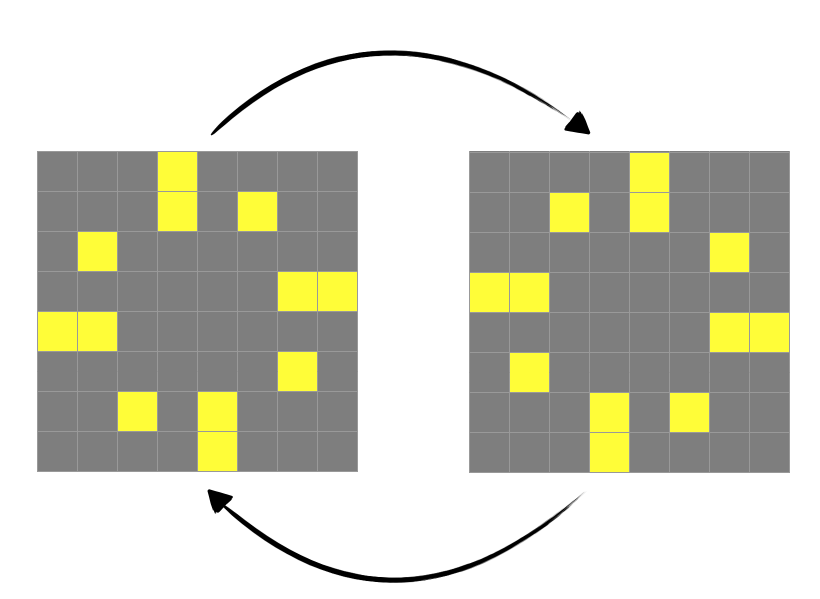
Prove that there is no oscillator of period \(4\) (i.e: the whole pattern repeats every \(4\) generations) which has exactly one cell that also has period \(4\).

A pattern \(P\) is called a garden of Eden if there exists no pattern \(P'\) distinct to \(P\) such that \(P'\) evolves into \(P\) after one generation. Show that a garden of Eden exists. You do not need to provide an example of such a pattern.

Every even number is not prime. The number \(9\) is not an even number, therefore it is not not prime, i.e: the number \(9\) is prime.

In a school there are three sports clubs, which we call \(A\), \(B\), and \(C\).

A student argues as follows:

“To find how many people attend at least one club, we can add the number of people in each club. However, students who attend all three clubs get counted three times. To fix this, we should subtract them twice. Therefore, the number of people who attend at least one club is \[\text{people in }A+\text{people in }B+\text{people in }C -2\times(\text{people in all three clubs}).\]”

Is this reasoning correct?

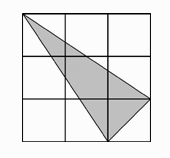
The diagram shows a triangle drawn on a square grid. The area of the shaded triangle is \(9~\text{cm}^2\). What is the area of one of the little squares of the grid?

The first \(2026\) prime numbers are multiplied. How many zeroes are at the end of this resulting number?

Three skiers—Alice, Bob, and Cynthia—compete in a downhill race. They begin skiing in the following order: first Cynthia, then Bob, and finally Alice.

Each skier starts with \(0\) points. Whenever one skier overtakes another during the race, the overtaking skier gains \(1\) point and the skier being overtaken loses \(1\) point.

At the end of the race, Alice crosses the finish line first, and Bob finishes with \(0\) points.

In what position does Cynthia finish?