Problems
What are the symmetries of the reduce-reuse-recycle symbol?
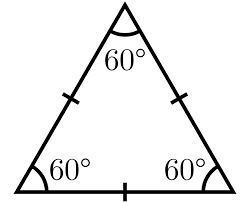
What are the symmetries of an equilateral triangle?
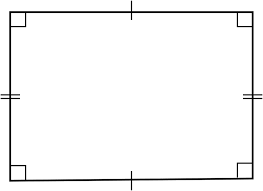
What are the symmetries of a rectangle (which is not a square)?
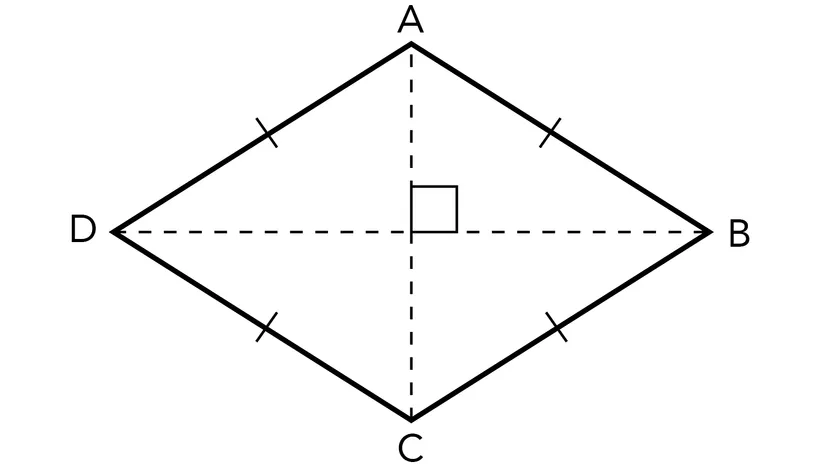
What are the symmetries of a rhombus (which isn’t a square)?
There are six symmetries of an equilateral triangle: three reflections, and three rotations (thinking of the identity as one the rotations).
Label the three reflections \(s_1\), \(s_2\) and \(s_3\). Label the identity by \(e\), rotation by \(120^{\circ}\) as \(r_1\), and rotation by \(240^{\circ}\) clockwise as \(r_2\).
What are the inverses of \(r_1\) and \(s_1\)?
Think about the symmetries of an equilateral triangle. We label rotation by \(120^{\circ}\) as \(r_1\), and reflection in the vertical median by \(s_1\).
Is applying \(r_1\), then \(s_1\) the same as applying \(s_1\), then \(r_1\)?
Let \(n\ge3\) be a positive integer. A regular \(n\)-gon is a polygon with \(n\) sides where every side has the same length, and every angle is the same. For example, a regular \(3\)-gon is an equilateral triangle, and a regular \(4\)-gon is a square.
What symmetries does a regular \(n\)-gon have, and how many?
The set of symmetries of an object (e.g. a square) is called a group. We can formally define a group \(G\) as follows.
A is a non-empty set \(G\) with a binary operation \(*:G\times G\to G\) satisfying the following axioms (you can think of them as rules that \(G\) and \(*\) have to satisfy). A binary operation takes two elements of \(G\) and gives another element of \(G\).
Associativity: For all \(g\), \(h\) and \(k\) in \(G\), \((g*h)*k=g*(h*k)\).
Identity: There is an element \(e\) of \(G\) such that \(e*g=g=g*e\) for all \(g\) in \(G\).
Inverses: For every \(g\) in \(G\), there exists a \(g^{-1}\) in \(G\) such that \(g*g^{-1}=e\).
Closure: For all \(g\) and \(h\) in \(G\), \(g*h\) is also in \(G\).
Prove that the symmetries of the ‘reduce-reuse-recycle’ symbol form a group.
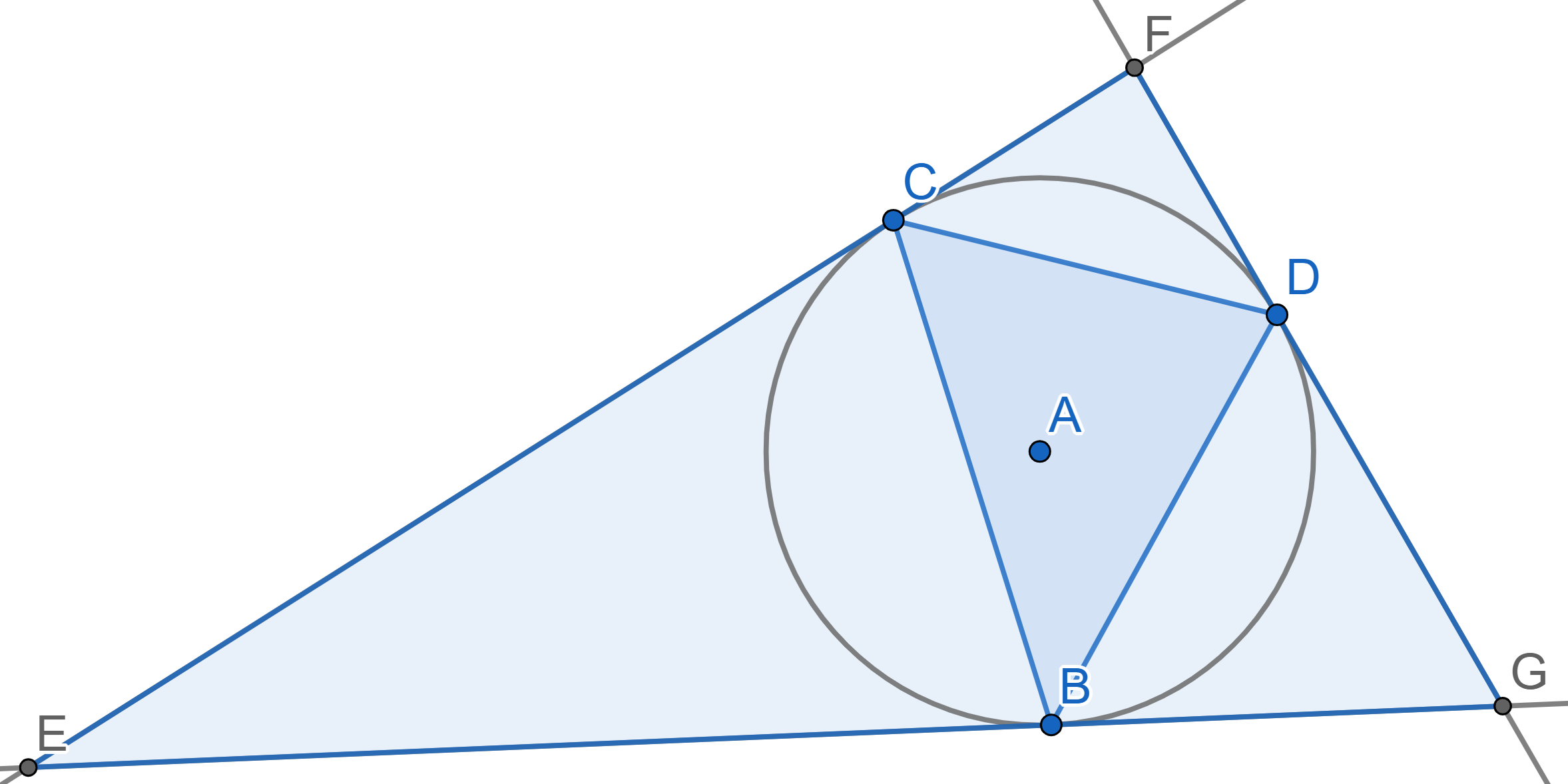
Consider the triangle \(BCD\), inscribed in a circle with center \(A\), the segments \(EF\), \(FG\), \(EG\) are tangent to the circle at the points \(C\), \(D\), \(B\) respectively. Prove that the Euler line of the triangle \(BCD\) passes through the center of the circle circumscribed around the triangle \(EFG\).
