Problems
Suppose \(x,y\) are real numbers such that \(x < y + \varepsilon\) for every \(\varepsilon > 0\). Show that \(x \leq y\).
What is logically the opposite of the statement “every \(n\) is odd or \(p<q\)"?
The picture below shows a closed disc, which is just a circle with the inside filled. The grey interior represents the interior of the disc. Describe the resulting shape when you glue the circular boundary to one point.

Label the vertices of a cube with the numbers \(1,2,3,\dots,8\) so that the sum of the labels of the four vertices of each of the six faces is the same.
Is it possible to construct a 485 × 6 table with the integers from 1 to 2910 such that the sum of the 6 numbers in each row is constant, and the sum of the 485 numbers in each column is also constant?
How many ways can the numbers \(1,1,1,1,1,2,3,\dots,9\) be listed in such a way that none of the \(1\)’s are adjacent? The number 1 appears five times and each of \(2\) to \(9\) appear exactly once.
John’s local grocery store sells 7 kinds of vegetable, 7 kinds of meat, 7 kinds of grains and 7 kinds of cheese. John would like to plan the entire week’s dinners so that exactly one ingredient of each type is used per meal and no ingredients repeat during the week. How many ways can John plan the dinners?
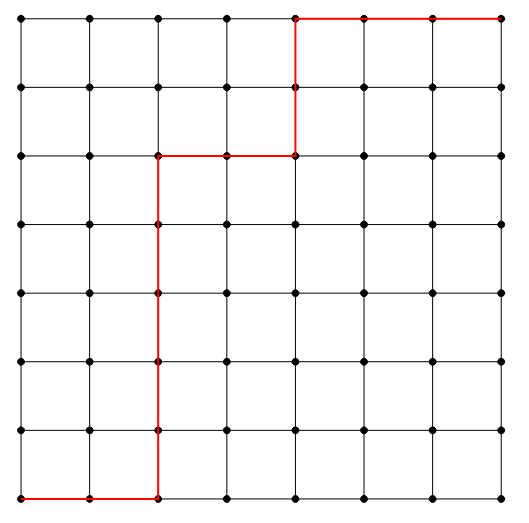
Suppose there is an \(7 \times 7\) grid. We would like to travel from the bottom left corner to the top right corner in exactly 14 steps. A step is from one point on the grid to another point via a segment of length 1. How many paths are there? The picture below shows one possible path on the grid.
In an office, at various times during the day, the boss gives the secretary a letter to type, each time putting the letter on top of the pile of the secretary’s in-box. When there is time, the secretary takes the top letter off the pile and types it. There are nine letters to be typed during the day, and the boss delivers them in the order \(1,2,3,4,5,6,7,8,9\). While leaving for lunch, the secretary tells a colleague that letter 8 has already been typed, but says nothing else about the morning’s typing. The colleague wonders which of the nine letters remain to be typed after lunch and in what order they will be typed. Base upon the above information, how many such after-lunch orders are possible? (That there are no letters left to be typed is one of the possibilities.)
A library keeps track of its books by a code with two (not necessarily different) letters taken from A to Z, followed by a three digit number from 000 to 999. What is the maximum number of books one can keep in the library and still tell them apart by looking at their codes?