Problems
Show that there are infinitely many composite numbers \(n\) such that \(3^{n-1}-2^{n-1}\) is divisible by \(n\).
Show that there are infinitely many numbers \(n\) such that \(2^n+1\) is divisible by \(n\). Find all prime numbers, that satisfy this property.
If \(k>1\), show that \(k\) does not divide \(2^{k-1}+1\). Find all prime numbers \(p,q\) such that \(2^p+2^q\) is divisible by \(pq\).
Find all positive integers \((x,n)\) such that \(x^n + 2^n + 1\) is a divisor \(x^{n+1} + 2^{n+1} + 1\).
Show that if \(n\) is an integer, greater than \(1\), then \(n\) does not divide \(2^n-1\).
Find all the integers \(n\) such that \(1^n + 2^n + ... + (n-1)^n\) is divisible by \(n\).
Take a pile of cards, Ace to 7 of Diamonds. Consider the following shuffle: simultaneously move the first card to the third position, the third card to the fifth position, the fifth card to the seventh position, and the seventh card to the first position. Also move the second card to the fourth position, the fourth card to the sixth position and the sixth card to the second position.
How many times do you have to do this specific shuffle in a row to get back to where you started?
How many permutations are there of 4 cards leaving no card in the same position as before?
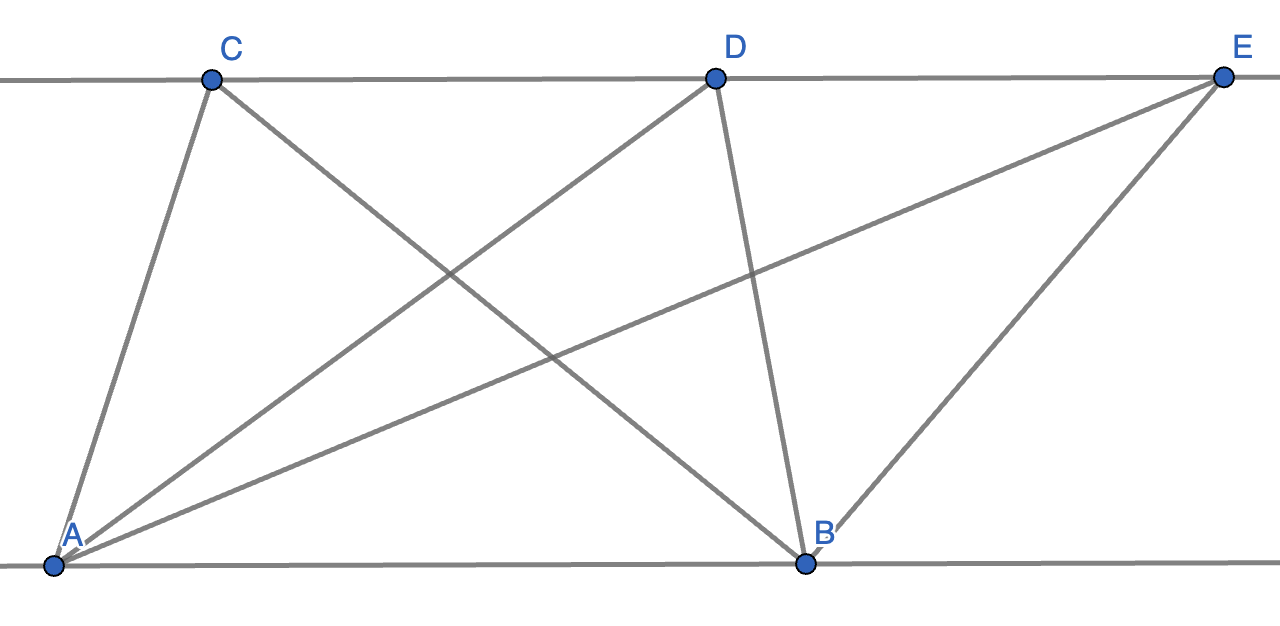
Lines \(AB\) and \(CDE\) are parallel. Which triangle out of \(\triangle ABC\), \(\triangle ABD\) and \(\triangle ABE\) has the greatest area?
