Problems
There is a secret gathering of a group of \(n\) aliens in a very dark room. You cannot see anyone in the room, but you hear the following questions.
“Is at least one of us a Goop?"
“Is the number of Goops amongst us an even number?"
“Is the number of Goops amongst us a multiple of 3?"
\(\dots\)
“Is the number of Goops amongst us a multiple of \(n\)?"
What are all the possible values of \(n\) such that this gathering can happen? Note that each of the \(n\) aliens have asked exactly one question.
You meet a group of \(n\) aliens. The first alien asks “is at least one of us a Goop?", the second alien asks “are at least two of us Goops?", the third asks “are at least three of us Goops?" and so on until the final one says “are at least \(n\) of us Goops?".
How many Goops are there?
Suppose you only knew the area formula of a triangle for right-angled triangles. That is, if a base with length \(b\) and a height \(h\) of a triangle meet at a right angle, you know that the area of the triangle is \(\frac{1}{2}bh\). Can you prove the usual area formula for a general triangle?
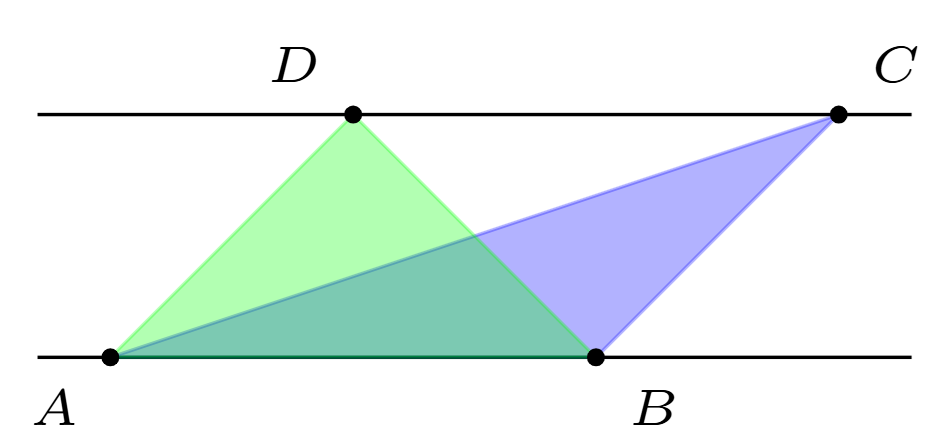
There is a pair of parallel lines. The point \(A\) and \(B\) lie on one of the lines. The point \(C\) and \(D\) lies on the other line. We can form triangles \(\triangle ABC\) and \(\triangle ABD\). Prove that the areas of triangles \(\triangle ABC\) and \(\triangle ABD\) are equal.
The pigeonhole principle is often called “Dirichlet’s box principle". Dirichlet made good use of this tool to show a fundamental result in Diophantine approximation, now commonly known as the Dirichlet Approximation Theorem. You will now prove it yourself!
Suppose \(\alpha\) is any irrational real number and \(N\geq 1\) is any positive integer. Show that there is an integer \(1\leq q\leq N\) and an integer \(p\) such that \[\left| q \alpha - p \right| < \frac{1}{N}.\]
What’s the sum of the Fibonacci numbers \(F_0+F_1+F_2+...+F_n\)?
What’s the sum \(\frac{F_2}{F_1}+\frac{F_4}{F_2}+\frac{F_6}{F_3}+...+\frac{F_{18}}{F_9}+\frac{F_{20}}{F_{10}}\)?
We have a sequence where the first term (\(x_1\)) is equal to \(2\), and each term is \(1\) minus the reciprocal of the previous term (which we can write as \(x_{n+1}=1-\frac{1}{x_n}\)).
What’s \(x_{57}\)?