Problems

Multiply an odd number by the two numbers either side of it. Prove that the final product is divisible by \(24\).

Mattia is thinking of a big positive integer. He tells you what this number to the power of \(4\) is. Unfortunately it’s so large that you tune out, and only hear that the final digit is \(4\). How do you know that he’s lying?

You might want to know what day of the week your birthday is this year. Mathematician John Conway invented an algorithm called the ‘Doomsday Rule’ to determine which day of the week a particular date falls on. It works by finding the ‘anchor day’ for the year that you’re working in. For \(2025\), the anchor day is Friday. Certain days in the calendar always fall on the anchor day. Some memorable ones are the following:
‘\(0\)’ of March - which is \(29\)th February in a leap year, and \(28\)th February otherwise.

\(4\)th April, \(6\)th June, \(8\)th August, \(10\)th October and \(12\)th December. These are easier to remember as \(4/4\), \(6/6\), \(8/8\), \(10/10\) and \(12/12\).

\(9\)th May, \(11\)th July, \(5\)th September and \(7\)th November. These are easier to see as \(9/5\), \(11/7\), \(5/9\) and \(7/11\). A mnemonic for them is “9-5 at the 7-11".
Then find the nearest one of these dates to the date that you’re looking for and find remainders.

For example, \(\pi\) day, (\(14\)th March, which is written \(3/14\) in American date notation. It’s also Albert Einstein’s birthday) is exactly \(14\) days after ‘\(0\)’th March, so is the same day of the week - Friday in \(2025\).

What day of the week will \(25\)th December be in \(2025\)?

\(6\) friends get together for a game of three versus three basketball. In how many ways can they be split into two teams? The order of the two teams doesn’t matter, and the order within the teams doesn’t matter.

That is, we count A,B,C vs. D,E,F as the same splitting as F,D,E vs A,C,B.

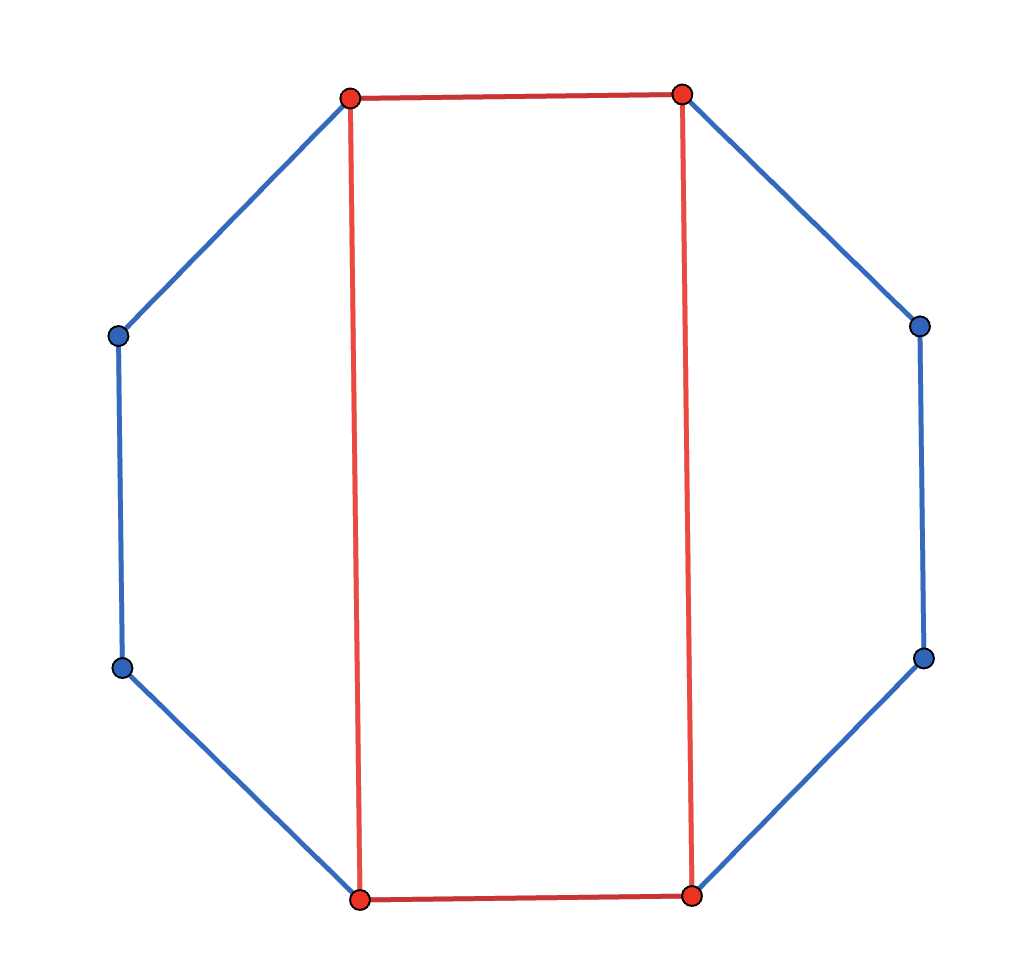
Below is a regular octagon. Given that its side length is \(1\), what’s the difference between the area of the red rectangle and the rest of the octagon?

\(x\), \(y\) and \(z\) are all integers. We’re told that \[\begin{align} x^3yz&=6\\ xy^3z&=24\\ xyz^3&=54. \end{align}\] What’s \(xyz\)?

In the diagram, all the small squares are of the same size. What fraction of the large square is shaded?

The letters \(O\), \(P\), \(S\) and \(T\) represent different digits from \(1\) to \(9\). The same letters correspond to the same digits, while different letters correspond to different digits.

Find \(O+P+S+T\), given that \(SPOT+POTS=15,279\).

A remainder is the number that is “left over" from division. Even if a number is not divisible by another number fully, we can still divide, but leaving a remainder. The remainder is less than the number we’re dividing by. For example, a remainder of \(44\) in division by \(7\) is \(2\), because \(44 = 6 \times 7 + 2\).

More generally, given any integer \(n\) and positive integer \(k\), we can always write \(n=qk+r\), where \(0\leq r<k\). We say that \(k\) goes into \(n\) \(q\) times, and a little bit (\(r\)) is left. If that little bit was larger than \(k\), it could “go into" \(n\) once more. This means we can always enforce the condition \(0\leq r<k\) on the remainder \(r\).

The general rule is that the remainder of a sum, difference or a product of two remainders is equal to the remainder of a sum, difference or a product of the original numbers. What that means is if we want to find a remainder of a product of two numbers, we need to look at the individual remainders, multiply them, and then take a remainder.

For example, \(10\) leaves the remainder \(3\) when divided by \(7\) and \(11\) leaves the remainder \(4\) when divided by \(7\). The product \(10\times11=110\) has the same remainder as the product of the individual remainders. We first multiply \(3\times4=12\) and then calculate the remainder upon division by \(7\), which is \(5\) because \(12=7+5\). That means that \(110\) gives a remainder of \(5\) when divided by \(7\). We can verify the result by calculating the remainder without simplifying first: \(110=15\times7+5\).

Here is a useful notation when discussing problems involving remainders and divisibility although it is not necessary for this problem sheet. Take two integers \(a\) and \(b\). If they differ by a multiple of a positive integer \(k\), then we write \(a \equiv b \pmod{k}\). For example, since \(24 - 10 = 2 \times 7\), we can express this fact by \(10 \equiv 24 \pmod{7}\). We say that 10 and 24 are congruent modulo 7.

Using this new notation, we can easily express the rules for remainders. Let \(a \equiv b \pmod{k}\) and \(c \equiv d \pmod{k}\). Then we have \(a + c \equiv b + d \pmod{k}\) and \(a \times c \equiv b \times d \pmod{k}\). As an example, again consider the calculation of the remainder of \(10 \times 11\) when divided by 7. We have \(10 \times 11 \equiv 3 \times 4 \equiv 12 \equiv 5 \pmod{7}\).

We make one last observation, which shows the utility of remainder when discussing divisibility. Saying that a number \(a\) is divisible by a number \(k\) is the same as saying the remainder of \(a\) when divided by \(k\) is 0. In congruence notation, the latter condition is \(a \equiv 0 \pmod{k}\).

Let’s have a look at some examples with remainders:

Picasso colours every point on the circumference of a circle red or blue. Is he guaranteed to create an equilateral triangle all of whose vertices are the same colour?