Problems

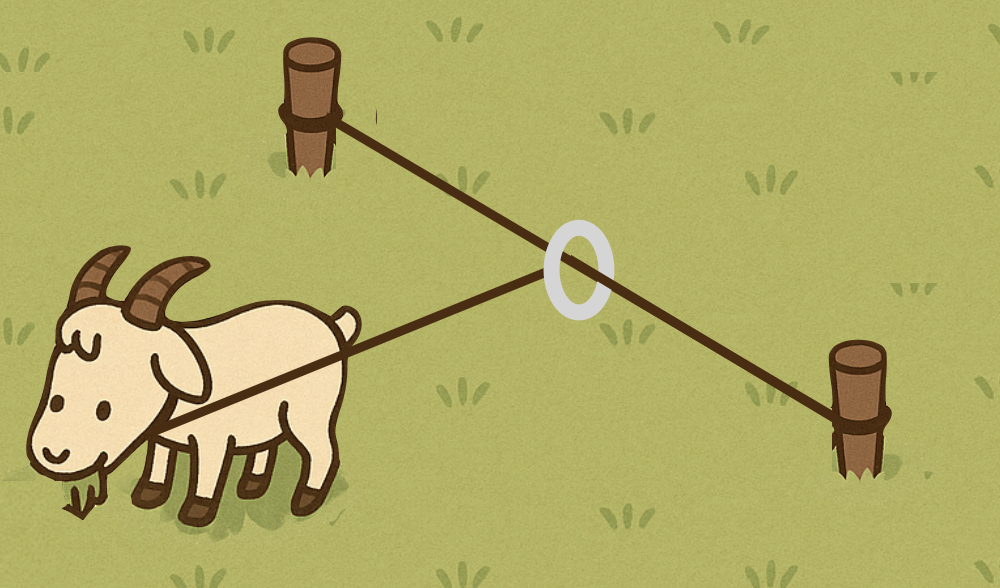
One day, Robinson Crusoe tied a rope tightly between two pegs, placed a sliding ring on it, and then tied the goat to the ring with another rope, as in the picture below. What shape did the goat graze this time?

On another day, Robinson Crusoe used two pegs again. This time, he tied one rope of length \(a\) to the first peg and another rope of length \(b\) to the second peg, both directly to the goat, so that it looked like in the picture below. What shape did the goat graze that day?

One day Robinson Crusoe went for a walk on a plateau, taking his goat with him on a rope of length one meter. He walked along a path in the shape of a rectangle measuring \(1 \,\text{km} \times 3 \,\text{km}\), following its perimeter. What was the shape of the area where the goat could graze while walking with Robinson?

Draw how Robinson Crusoe should use pegs, ropes, and sliding rings to tie his goat in order for the goat to graze grass in the shape of a semicircle.

Draw a picture how Robinson could have used pegs and ropes to tie the wolf and the goat so that the goat grazed an area in the shape of a ring (like a disc with a hole in the middle).

Think of other shapes Robinson’s goat can graze without a wolf, or with a wolf tied nearby. What if Robinson managed to tame several wolves and used them as guard dogs? Can two tied wolves keep an untied goat in a triangle? Can you think of other shapes you can create with Robinson’s goat and wolves?

Prove the divisibility rule for \(3\): a number is divisible by \(3\) if and only if the sum of its digits is divisible by \(3\).

Sophia is playing the following game: she chooses a whole number, and then she writes down the product of all the numbers from \(1\) up to the number she chose. For example, if she chooses \(5\), then she writes down \(1\times 2 \times 3 \times 4 \times 5\). What is the smallest number she can choose for her game, such that the result she gets in the end is divisible by \(2024\)?

While studying numbers and their properties, Robinson came across a three-digit prime number whose last digit equals the sum of the first two digits. What are the options for the last digit of this number, given that none of its digits is zero?

Prove the divisibility rule for \(4\): a number is divisible by \(4\) if and only if the number made by the last two digits of the original number is divisible by \(4\);
Can you come up with a divisibility rule for \(8\)?