We solve problems

Problems Discrete Mathematics Set theory and logic Mathematical logic Mathematical logic (other)

The seller with weights. With four weights the seller can weigh any integer number of kilograms, from 1 to 40 inclusive. The total mass of the weights is 40 kg. What are the weights available to the seller?

Problem #PRU-102841

Problems Discrete Mathematics Set theory and logic Mathematical logic Mathematical logic (other)

11–12 2.0

Two weighings. There are 7 coins which are identical on the surface, including 5 real ones (all of the same weight) and 2 counterfeit coins (both of the same weight, but lighter than the real ones). How can you find the 3 real coins with the help of two weighings on scales without weights?

Problem #PRU-102845

Problems Discrete Mathematics Combinatorics Dissections, partitions, covers and tilings Dissections with certain properties

11–12 2.0

Cutting into four parts. Cut each of the figures below into four equal parts (you can cut along the sides and diagonals of cells).

Problem #PRU-102852

Problems Discrete Mathematics Set theory and logic Mathematical logic Mathematical logic (other)

11–12 2.0

We are looking for the correct statement. In a notebook one hundred statements are written:

1) There is exactly one false statement in this notebook.

2) There are exactly two false statements in this notebook.

...

100) There are exactly one hundred false statements in this notebook.

Which of these statements is true, if it is known that only one is true?

Problem #PRU-102854

Problems Discrete Mathematics Set theory and logic Mathematical logic Puzzles

11–12 2.0

Solve the rebus \(AC \times CC \times K = 2002\) (different letters correspond to different integers and vice versa).

Problem #PRU-102861

Problems Discrete Mathematics Set theory and logic Mathematical logic Puzzles

11–12 2.0

Rebus. Solve the numerical rebus \(AAAA-BBB + SS-K = 1234\) (different letters correspond to different numbers, but the same letters each time correspond to the same numbers)

Problem #PRU-102862

Problems Discrete Mathematics Algorithm Theory Theory of algorithms (other)

10–12 2.0

Multiplication of numbers. Restore the following example of the multiplication of natural numbers if it is known that the sum of the digits of both factors is the same.

Problem #PRU-102863

Problems Discrete Mathematics Algorithm Theory Theory of algorithms (other)

10–12 2.0

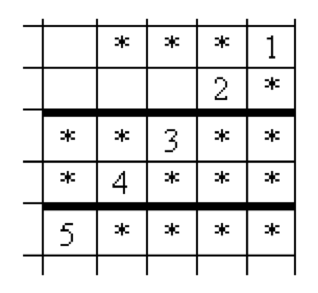
Restore the example of the multiplication.

Problem #PRU-102964

Problems Discrete Mathematics Algorithm Theory Game theory Game theory (other) Number Theory Divisibility Odd and even numbers

10–12 2.0

Petya and Misha play such a game. Petya takes in each hand a coin: one – 10 pence, and the other – 15. After that, the contents of the left hand are multiplied by 4, 10, 12 or 26, and the contents of the right hand – by 7, 13, 21 or 35. Then Petya adds the two results and tells Misha the result. Can Misha, knowing this result, determine which hand – the right or left – contains the 10 pence coin?

Problem #PRU-102965

Problems Discrete Mathematics Combinatorics Dissections, partitions, covers and tilings Tilings with ordinary and domino tiles

10–11 2.0

Giuseppe has a sheet of plywood, measuring \(22 \times 15\). Giuseppe wants to cut out as many rectangular blocks of size \(3 \times 5\) as possible. How should he do it?