Problems
In any group of 10 children, out of a total of 60 pupils, there will be three who are in the same class. Will it always be the case that amongst the 60 pupils there will be: 1) 15 classmates? 2) 16 classmates?
A pedestrian walked along six streets of one city, passing each street exactly twice, but could not get around them, having passed each one only once. Could this be?
When Harvey was asked to come up with a problem for the mathematical Olympiad in Sunny City, he wrote a rebus (see the drawing). Can it be solved? (Different letters must match different numbers).
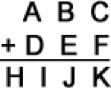
One term a school ran 20 sessions of an after-school Astronomy Club. Exactly five pupils attended each session and no two students encountered one another over all of the sessions more than once. Prove that no fewer than 20 pupils attended the Astronomy Club at some point during the term.
In the rebus below, replace the letters with numbers such that the same numbers are represented with the same letter. The asterisks can be replaced with any numbers such that the equations hold.
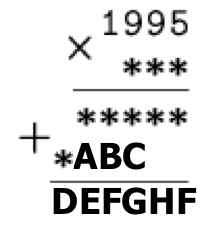
An explanation of the notation used: the unknown numbers in the third and fourth rows are the results of multiplying 1995 by each digit of the number in the second row, respectively. These third and fourth rows are added together to get the total result of the multiplication \(1995 \times ***\), which is the number in the fifth row. This is an example of a “long multiplication table”.
In two purses lie two coins, and one purse has twice as many coins as the other. How can this be?
Which five-digit numbers are there more of: ones that are not divisible by 5 or those with neither the first nor the second digit on the left being a five?
Three people A, B, C counted a bunch of balls of four colors (see table).
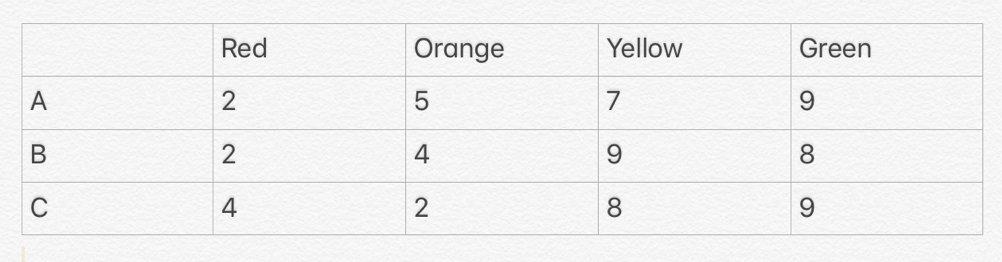
Each of them correctly distinguished some two colors, and confused the numbers of the other two colours: one mixed up the red and orange, another – orange and yellow, and the third – yellow and green. The results of their calculations are given in the table.
How many balls of each colour actually were there?
Alex laid out an example of an addition of numbers from cards with numbers on them and then swapped two cards. As you can see, the equality has been violated. Which cards did Alex rearrange?
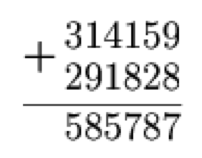
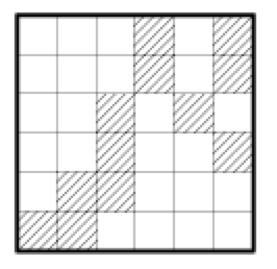
Cut the board shown in the figure into four congruent parts so that
each of them contains three shaded cells. Where the shaded cells are
placed in each part need not be the same.