Problems
Know-it-all came to visit the twin brothers Screw and Nut, knowing that one of them never speaks the truth, and asked one of them: “Are you Screw?”. “Yes,” he replied. When Know-it-all asked the second brother the same question, he received an equally clear answer and immediately determined who was who.
Who was called Screw?
A resident of one foreign intelligence agency informed the centre about the forthcoming signing of a number of bilateral agreements between the fifteen former republics of the USSR. According to his report, each of them will conclude an agreement exactly with three others. Should this resident be trusted?
Uncle Jack, the cat Whiskers, Spot and postman Pat are sitting on a bench. If Spot, sitting to the right of everyone, sits between Uncle Jack and the cat, then the cat will be at the extreme left. In what order do they sit?
Cut a square into three pieces, from which you can construct a triangle with three acute angles and three different sides.
In any group of 10 children, out of a total of 60 pupils, there will be three who are in the same class. Will it always be the case that amongst the 60 pupils there will be: 1) 15 classmates? 2) 16 classmates?
A pedestrian walked along six streets of one city, passing each street exactly twice, but could not get around them, having passed each one only once. Could this be?
When Harvey was asked to come up with a problem for the mathematical Olympiad in Sunny City, he wrote a rebus (see the drawing). Can it be solved? (Different letters must match different numbers).
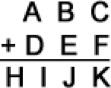
One term a school ran 20 sessions of an after-school Astronomy Club. Exactly five pupils attended each session and no two students encountered one another over all of the sessions more than once. Prove that no fewer than 20 pupils attended the Astronomy Club at some point during the term.
In the rebus below, replace the letters with numbers such that the same numbers are represented with the same letter. The asterisks can be replaced with any numbers such that the equations hold.
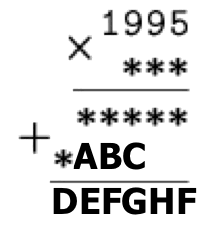
An explanation of the notation used: the unknown numbers in the third and fourth rows are the results of multiplying 1995 by each digit of the number in the second row, respectively. These third and fourth rows are added together to get the total result of the multiplication \(1995 \times ***\), which is the number in the fifth row. This is an example of a “long multiplication table”.
In two purses lie two coins, and one purse has twice as many coins as the other. How can this be?