Problems
On the island of Contrast, both knights and liars live. Knights always tell the truth, liars always lie. Some residents said that the island has an even number of knights, and the rest said that the island has an odd number of liars. Can the number of inhabitants of the island be odd?
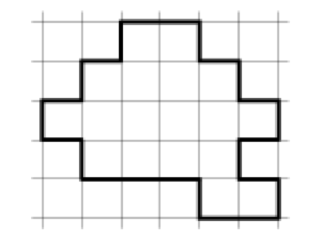
Cut the figure (on the boundaries of cells) into three equal parts (the same in shape and size).
In the line of numbers and signs \({}* 1 * 2 * 4 * 8 * 16 * 32 * 64 = 27\) position the signs “\(+\)” or “\(-\)” instead of the signs “\(*\)”, so that the equality becomes true.
The code of lock is a two-digit number. Ben forgot the code, but he remembers that the sum of the digits of this number, combined with their product, is equal to the number itself. Write all possible code options so that Ben could open the lock quickly.
Solve the problem: \(AX \times UX = 2001\). Both \(X\) stand for the same digit, but \(A\), \(U\) and \(X\) are all different single digits.
Solve the puzzle: \(BAO \times BA \times B = 2002\).
Jessica, Nicole and Alex received 6 coins between them: 3 gold coins and 3 silver coins. Each of them received 2 coins. Jessica doesn’t know which coins the others received but only which coins she has. Think of a question which Jessica can answer with either “yes”, “no” or “I don’t know” such that from the answer you can know which coins Jessica has.
Find the smallest four-digit number \(CEEM\) for which there exists a solution to the rebus \(MN + PORG = CEEM\). (The same letters correspond to the same numbers, different – different.)
A space traveller decided to visit the planet and upon arrival he met three inhabitants. The traveller asked each of the inhabitants: “How many truth tellers are there among your companions?”. The first one answered: “None.” The second one said: “One”. What did the third alien say?
A rectangle is cut into several smaller rectangles, the perimeter of each of which is an integer number of meters. Is it true that the perimeter of the original rectangle is also an integer number of meters?