Problems
a) Prove that in any football team there are two players who were born on the same day of the week.
b) Prove that in the population of London, which is almost 9 million, there will be ten thousand people who celebrate their birthday on the same day.
Kai has a piece of ice in the shape of a “corner” (see the figure). The Snow Queen demanded that Kai cut it into four equal parts. How can he do this?
The king made a test for the future groom of his daughter. He put the princess in one of three rooms, a tiger in the other, and left the last room empty. It is known that the sign on the door where the princess is sitting is true, where the tiger is – it is false, and nothing is known about the sign on the third room. The tablets are as follows:
1 – room 3 is empty
2 – the tiger is in room 1
3 – this room is empty
Can the prince correctly guess the room with the princess?
On Easter Island, people ask each other questions, to which only “yes” or “no” can be answered. In this case, each of them belongs exactly to one of the tribes either A or B. People from tribe A ask only those questions to which the correct answer is “yes”, and from tribe B – those questions to which the correct answer is “no.” In one house lived a couple Ethan and Violet Russell. When Inspector Krugg approached the house, the owner met him on the doorstep with the words: “Tell me, do Violet and I belong to tribe B?”. The inspector thought and gave the right answer. What was the right answer?
a) A 1 or a 0 is placed on each vertex of a cube. The sum of the 4 adjacent vertices is written on each face of the cube. Is it possible for each of the numbers written on the faces to be different?
b) The same question, but if 1 and \(-1\) are used instead.
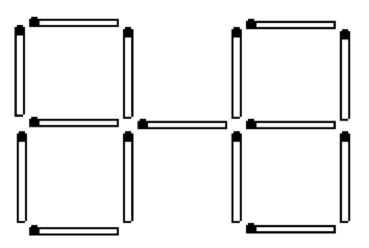
a) In the construction in the figure, move two matches so that there are five identical squares created. b) From the new figure, remove 3 matches so that only 3 squares remain.
How many squares are shown in the picture?
Gerard says: the day before yesterday I was 10 years old, and next year I will turn 13. Can this be?
We call a natural number “amazing” if it has the form \(a^b + b^a\) (where \(a\) and \(b\) are natural numbers). For example, the number 57 is amazing, since \(57 = 2^5 + 5^2\). Is the number 2006 amazing?
Homework. Cut a hole in an exercise book of a size so that you yourself can climb through it.