Problems

a) In how many ways can Dima paint five Christmas trees in silver, green and blue colours, if the amount of paint is unlimited, and he paints each tree in only one colour?

b) Dima has five baubles: a red, a green, a yellow, a blue and a gold one. In how many ways can he decorate five Christmas trees with them, if he needs to put exactly one bauble on each tree?

c) What about if he can hang several baubles on one Christmas tree (and all of the baubles have to be used)?

A toddler has \(25\) lego pieces in a box:

• In how many ways are there to choose three pieces to play with?

• In how many ways can he choose three pieces for the foundation, main walls and roof? Note that the order is important.

Doctor Smith gave out 2006 miracle tablets to four sick animals. The rhinoceros received one more tablet than the crocodile. The hippopotamus got one more tablet than the rhino. The elephant got one more tablet than the hippo. How many tablets did the elephant have to eat?

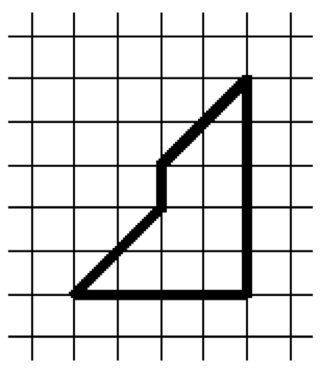
Cut the shape (see the figure) into two identical pieces (coinciding when placed on top of one another).

Gabby is standing on a river bank. She has two clay jars: one – for 5 litres, and about the second Gabby remembers only that it holds either 3 or 4 litres. Help Gabby determine the capacity of the second jar. (Looking into the jar, you cannot figure out how much water is in it.)

There are two numbers \(x\) and \(y\) being added together. The number \(x\) is less than the sum \(x+y\) by 2000. The sum \(x+y\) is bigger than \(y\) by 6. What are the values of \(x\) and \(y\)?

On Brennan’s birthday, the postman Daniel wants to find out how old Brennan is. Sarah says that Brennan is over 11 years old, and Matt claims that he is more than 10 years old. How old is Brennan, if it is known that exactly one of them was mistaken? Justify your answer.

In the garden of Sandra and Lewis 2006 rose bushes were growing. Lewis watered half of all the bushes, and Sandra watered half of all the bushes. At the same time, it turned out that exactly three bushes, the most beautiful, were watered by both Sandra and Lewis. How many rose bushes have not been watered?

The digits of a 3 digit number \(A\) were written in reverse order and this is the number \(B\). Is it possible to find a value of \(A\) such that the sum of \(A\) and \(B\) has only odd numbers as its digits?

In a burrow there is a family of 24 mice. Every night exactly four of them are sent to the warehouse for cheese.

Could it occur that at some point in time each mouse went to the warehouse with every other mouse exactly one time?