We solve problems

Problem #PRU-109527

Problems Fun Problems Word Problems Tables and tournaments Methods Tables and tournaments (other) Pigeonhole principle Pigeonhole principle (other) Proof by contradiction

11–13 3.0

What is the largest number of counters that can be put on the cells of a chessboard so that on each horizontal, vertical and diagonal (not only on the main ones) there is an even number of counters?

Problem #PRU-109754

Problems Geometry Solid geometry Visual geometry in space

11–13 2.0

Prove that for all \(x \in (0;\pi /2)\) for \(n > m\), where \(n, m\) are natural, we have the inequality \(2 | \sin^n x-\cos^n x | \leq 3 | \sin^m x-\cos^m x |\);

Problem #PRU-109766

Problems Fun Problems Word Problems Tables and tournaments Methods Number tables and its properties Pigeonhole principle Pigeonhole principle (other)

12–14 4.0

Is it possible to arrange natural numbers from 1 to \(2002^2\) in the cells of a \(2002\times2002\) table so that for each cell of this table one could choose a triplet of numbers, from a row or column, where one of the numbers is equal to the product of the other two?

Problem #PRU-109808

Problems Discrete Mathematics Combinatorics Geometry on grid paper Integer lattices Integer lattices (other) Painting problems Methods Pigeonhole principle Pigeonhole principle (finite number of poits, lines etc.)

12–14 3.0

All of the points with whole number co-ordinates in a plane are plotted in one of three colours; all three colours are present. Prove that there will always be possible to form a right-angle triangle from these points so that its vertices are of three different colours.

Problem #PRU-109877

Problems Methods Pigeonhole principle (finite number of poits, lines etc.) Pigeonhole principle

11–13 3.0

A regular hexagon with sides of length \(5\) is divided by straight lines, that are parallel to its sides, to form regular triangles with sides of length 1. We call the vertices of all such triangles nodes. It is known that more than half of the nodes are marked. Prove that there are five marked nodes lying on one circle.

Problem #PRU-109909

Problems Algorithm Theory Theory of algorithms (other) Discrete Mathematics

10–12 2.0

Members of the State parliament formed factions in such a way that for any two factions \(A\) and \(B\) (not necessarily different)

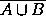
– also a faction (through

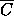
the set of all parliament members not included in \(C\) is denoted). Prove that for any two factions \(A\) and \(B\), \(A \cup % \includegraphics{https://problems-static.s3.amazonaws.com/production/problem_images/109909-3.png} B\) is also a faction.

Problem #PRU-110072

Problems Methods Geometry on grid paper Pigeonhole principle (finite number of poits, lines etc.) Pigeonhole principle Discrete Mathematics Combinatorics Dissections, partitions, covers and tilings Dissections with certain properties

12–14 4.0

A target consists of a triangle divided by three families of parallel lines into 100 equilateral unit triangles. A sniper shoots at the target. He aims at a particular equilateral triangle and either hits it or hits one of the adjacent triangles that share a side with the one he was aiming for. He can see the results of his shots and can choose when to stop shooting. What is the largest number of triangles that the sniper can guarantee he can hit exactly 5 times?

Problem #PRU-110083

Problems Discrete Mathematics Combinatorics Painting problems Methods Pigeonhole principle Pigeonhole principle (finite number of poits, lines etc.) Fun Problems Word Problems Tables and tournaments Tables and tournaments (other)

12–14 3.0

Can the cells of a \(5 \times 5\) board be painted in 4 colours so that the cells located at the intersection of any two rows and any two columns are painted in at least three colours?

Problem #PRU-110103

Problems Methods Divisibility Division with remainders. Arithmetic of remainders Arithmetic of remainders Number Theory Pigeonhole principle Pigeonhole principle (other)

12–14 4.0

Is it possible to arrange the numbers 1, 2, ..., 60 in a circle in such an order that the sum of every two numbers, between which lies one number, is divisible by 2, the sum of every two numbers between which lie two numbers, is divisible by 3, the sum of every two numbers between which lie six numbers, is divisible by 7?

Problem #PRU-110166

Problems Algorithm Theory Methods Balance puzzles Pigeonhole principle Pigeonhole principle (other) Discrete Mathematics

12–14 4.0

A set of weights has the following properties: It contains \(5\) weights, which are all different in weight. For any two weights, there are two other weights of the same total weight. What is the smallest number of weights that can be in this set?