Problems
In the \(4 \times 4\) square, the cells in the left half are painted black, and the rest – in white. In one go, it is allowed to repaint all cells inside any rectangle in the opposite colour. How, in three goes, can one repaint the cells to get the board to look like a chessboard?
The sequence \(a_1, a_2, \dots\) is such that \(a_1 \in (1,2)\) and \(a_{k + 1} = a_k + \frac{k}{a_k}\) for any positive integer \(k\). Prove that it cannot contain more than one pair of terms with an integer sum.The sequence \(a_1, a_2, \dots\) is such that \(a_1 \in (1,2)\) and \(a_{k + 1} = a_k + \frac{k}{a_k}\) for any positive integer \(k\). Prove that it cannot contain more than one pair of terms with an integer sum.
Prove that if the expression
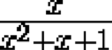
takes a rational value, then the expression
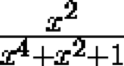
also takes on a rational value.
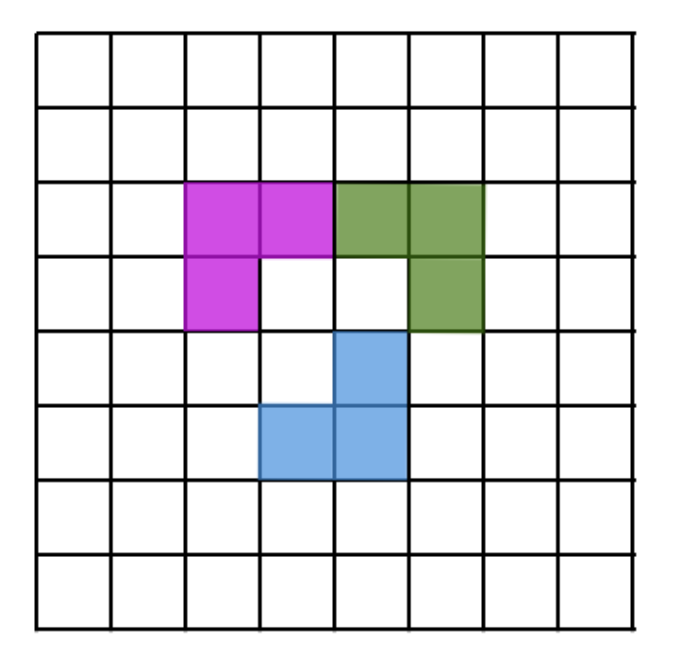
On an 8×8 grid (like a chessboard), an L-corner is a shape made of 3 little squares of the board that touch to make an L. You can turn the L any way you like. We place the L-corners so that none overlap. What is the fewest L-corners you must place so that no more L-corners can be added anywhere? Here is an example of how three L-corners may look like:
An airline flew exactly 10 flights each day over the course of 92 days. Each day, each plane flew no more than one flight. It is known that for any two days in this period there will be exactly one plane which flew on both those days. Prove that there is a plane that flew every day in this period.
The product of two natural numbers, each of which is not divisible by 10, is equal to 1000. Find the sum of these two numbers.
10 children, including Billy, attended Billy’s birthday party. It turns out that any two children picked from those at the party share a grandfather. Prove that 7 of the children share a grandfather.
An old analogue clock speeds up by 9 minutes after 24 hours. If you went to sleep at 22:00 and set the correct time on the clock, then for what time should the alarm be set if you want it to go off at exactly 6:00? Explain your answer.
A class has 25 pupils. It is known that for any two girls in the class, the number of male friends they have in the class is different. What is the maximum number of girls that it is possible for there to be in the class?
In the king’s prison, there are five cells numbered from 1 to 5. In each cell, there is one prisoner. Kristen persuaded the king to conduct an experiment: on the wall of each cell she writes at one point a number and at midnight, each prisoner will go to the cell with the indicated number (if the number on the wall coincides with the cell number, the prisoner does not go anywhere). On the following night at midnight, the prisoners again must move from their cell to another cell according to the instructions on the wall, and they do this for five nights. If the location of prisoners in the cells for all six days (including the first) is never repeated, then Kristen will be given the title of Wisdom, and the prisoners will be released. Help Kristen write numbers in the cells.