Problems
Cambria was various cuboids from \(1\times 1\times1\) cubes. She initially built one cuboid, then increased its length and width by \(1\) and reduced its height by \(2\). She noticed that she needed the same number of \(1\times 1\times 1\) cubes to build both the original and new cuboids. Show that the number of cubes used for each of the cuboids is divisible by \(3\).
Is it possible to cut an equilateral triangle into three equal hexagons?
A labyrinth was drawn on a \(5\times
5\) grid square with an outer wall and an exit one cell wide, as
well as with inner walls running along the grid lines. In the picture,
we have hidden all the inner walls from you (We give you several copies
to facilitate drawing) 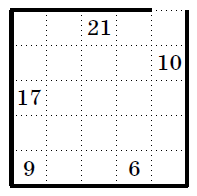


Please draw how the walls were arranged. Keep in mind that the numbers
in the cells represent the smallest number of steps needed to exit the
maze, starting from that cell. A step can be taken to any adjacent cell
vertically or horizontally, but not diagonally (and only if there is no
wall between them, of course).
Is it possible to cut this figure, called "camel"
a) along the grid lines;
b) not necessarily along the grid lines;
into \(3\) parts, which you can use
to build a square?
(We give you several copies to facilitate drawing)



Michael used different numbers \(\{0,1,2,3,4,5,6,7,8,9\}\) to put in the
circles in the picture below, without using any one of them twice.
Inside each triangle he wrote down either the sum or the product of the
numbers at its vertices. Then he erased the numbers in the circles.
Which numbers need to be written in circles so that the condition is
satisfied?
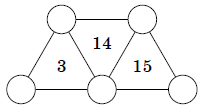
Find all solutions to the puzzle \(\textrm{AC}\times\textrm{CC}\times\textrm{K} = 2002.\) Different letters correspond to different digits, identical letters correspond to identical digits. Find all solutions.
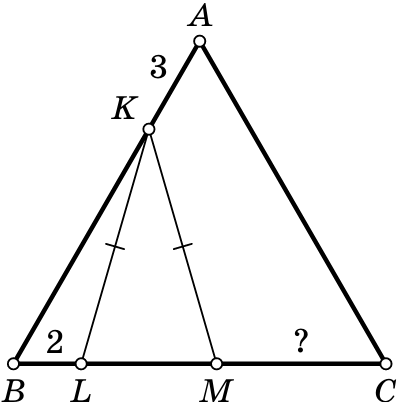
The triangle \(ABC\) is equilateral.
The point \(K\) is chosen on the side
\(AB\) and points \(L\) and \(M\) are on the side \(BC\) in such a way that \(L\) lies on the segment \(BM\). We have the following properties:
\(KL = KM,\) \(BL = 2,\, AK = 3.\) Find the length of
\(CM\).
We call two figures congruent if their corresponding sides and angles are equal. Let \(ABD\) an \(A'B'D'\) be two right-angled triangles with right angle \(D\). Then if \(AD=A'D'\) and \(AB=A'B'\) then the triangles \(ABD\) and \(A'B'D'\) are congruent.
It follows from the previous statement that if two lines \(AB\) and \(CD\) are parallel than angles \(BCD\) and \(CBA\) are equal.
We prove the other two assertions from the description:
The sum of all internal angles of a triangle is also \(180^{\circ}\).
In an isosceles triangle (which has two sides of equal lengths), two angles touching the third side are equal.
In the triangle \(ABC\) the sides are compared as following: \(AC>BC>AB\). Prove that the angles are compared as follows: \(\angle B > \angle A > \angle C\).