Problems
Winnie the Pooh has five friends, each of whom has pots of honey in their house: Tigger has \(1\) pot, Piglet has \(2\), Owl has \(3\), Eeyore has \(4\), and Rabbit has \(5\). Winnie the Pooh comes to visit each friend in turn, eats one pot of honey and takes the other pots with him. He came into the last house carrying \(10\) pots of honey. Whose house could Pooh have visited last?
Find the largest possible number of bishops that can be placed on the \(8 \times 8\) chessboard so that no two bishops threaten each other.
Does there exist a power of \(3\) that ends in \(0001\)?
There are \(24\) children in a class. Some pairs of children are friends. The friendship relation satisfies the following rules:
If someone (say Alice) is a friend of someone else (say Bob), then Bob is a friend of Alice.
If Alice is a friend of Bob and Bob is a friend of Claire, then Alice is also a friend of Claire.
Therefore Alice must be friends with herself. Is this reasoning correct?
I am going to convince you that all people have the same eye color! How? Well, notice that if there were only one person in the world, then my claim would be true. Now we will explain that if the claim is true when there are \(n\) people in the world, then it will also be true when there are \(n+1\) people. Therefore, it will be true regardless of the amount of people! (This kind of proof is called a proof by induction)
Let’s imagine that the claim is true when there are \(n\) people in the world. Now take any group of \(n+1\) people, and label them \(a_1,a_2,\dots,a_{n+1}\). Remove \(a_1\). The remaining people \(a_2,a_3,\cdots,a_{n+1}\) form a group of \(n\) people, so they must all have the same eye colour.
On the other hand, let’s remove \(a_{n+1}\). The remaining people \(a_1,a_2,\dots,a_{n}\) also form a group of \(n\) people, so they must again all have the same eye colour.
Since these two smaller groups overlap (they both contain \(a_2,a_3,\dots,a_{n-1}\)), everyone in the full group \(a_1,a_2,\dots,a_n\) has the same eye colour.
We are going to show that \(1\) is
the largest natural number.
Proof: Let \(n\) be the largest natural
number. We will show that \(n=1\).
Since \(n\) is the largest natural
number, \(n^2\), which is also a
natural number, must be less than or equal to \(n\). Therefore \(n^2-n\leq 0\). But \(n^2-n=n(n-1)\). If \(n(n-1)\leq 0\), it must be that \(0\leq n\leq 1\), and so \(n=1\).
Theorem: If we mark \(n\) points on
a circle and connect each point to every other point by a straight line,
the lines divide the interior of the circle is into is \(2n-1\) regions.
"Proof": First, let’s have a look at the smallest natural numbers.
When \(n=1\) there is one region (the whole disc).
When \(n=2\) there are two regions (two half-discs).
When \(n=3\) there are \(4\) regions (three lune-like regions and one triangle in the middle).
When \(n=4\) there are \(8\) regions, and if you’re still not convinced then try \(n=5\) and you’ll find \(16\) regions if you count carefully.
Our proof in general will be by induction on \(n\). Assuming the theorem is true for \(n\) points, consider a circle with \(n+1\) points on it. Connecting \(n\) of them together in pairs produces \(2n-1\) regions in the disc, and then connecting the remaining point to all the others will divide the previous regions into two parts, thereby giving us \(2\times (2n-1)=2n\) regions.
Let’s "prove" that the number \(1\) is a multiple of \(3\). We will use the symbol \(\equiv\) to denote "congruent modulo \(3\)". Thus, what we need to prove is that \(1\equiv 0\) modulo \(3\). Let’s see: \(1\equiv 4\) modulo \(3\) means that \(2^1\equiv 2^4\) modulo \(3\), thus \(2\equiv 16\) modulo \(3\), however \(16\) gives the remainder \(1\) after division by \(3\), thus we get \(2\equiv 1\) modulo \(3\), next \(2-1\equiv 1-1\) modulo \(3\), and thus \(1\equiv 0\) modulo \(3\). Which means that \(1\) is divisible by \(3\).
Recall that \((n+1)^2=n^2+2n+1\). Subtracting \(2n+1\) from both sides gives \((n+1)^2-(2n+1)=n^2\). Now subtract \(n(2n+1)\) from both sides to obtain \((n+1)^2-(2n+1)-n(2n+1)=n^2-n(2n+1)\). Notice that the left-hand side can be rewritten as \((n+1)^2-(n+1)(2n+1)\), so we have \((n+1)^2-(n+1)(2n+1)=n^2-n(2n+1)\).
Next, add \(\frac{(2n+1)^2}{4}\) to both sides. This allows us to complete the square on each side, giving \(((n+1)-\frac{2n+1}{2})^2=(n-\frac{2n+1}{2})^2\).
Taking square roots of both sides leads to \((n+1)-\frac{2n+1}{2}=n-\frac{2n+1}{2}\). Adding \(\frac{2n+1}{2}\) to both sides produces \(n+1=n\), which simplifies to \(1=0\).
Look at the diagram below, which shows how to rearrange the pieces forming the first triangle.
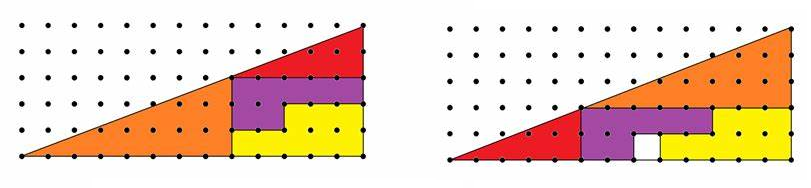
The shape seems unchanged, yet after looking more closely, we see that
the second picture appears to contain one extra square of area. How can
this be?