Problems

On board the airplane there are \(2n\) passengers, and the airline loaded for them \(n\) servings of lunch with chicken and \(n\) servings with fish. It is known that a passenger with a probability of 0.5 prefers chicken and with a probability of 0.5 prefers fish. Let’s call a passenger dissatisfied if he does not have what he prefers.

a) Find the most likely number of dissatisfied passengers.

b) Find the mathematical expectation of the number of dissatisfied passengers.

c) Find the variance of the number of dissatisfied passengers.

In Anchuria, there is a single state examination. The probability of guessing the correct answer to each exam question is 0.25. In 2011, in order to obtain a certificate, it was necessary to answer correctly to 3 questions out of 20. In 2012, the Anchuria School of Management decided that 3 questions were not enough. Now you need to correctly answer 6 questions out of 40. It is asked, if you do not know anything but just guess the answers, in what year is the probability of obtaining an Anchurian certificate higher: in 2011 or 2012?

James bought \(n\) pairs of identical socks. For \(n\) days James did not have any problems: every morning he took a new pair of socks out of the closet and wore it all day. After \(n\) days, James’ father washed all of the socks in the washing machine and put them into pairs in any way possible as, we repeat, all of the socks are the same. Let’s call a pair of socks successful, if both socks in this pair were worn by James on the same day.

a) Find the probability that all of the resulting pairs are successful.

b) Prove that the expectation of the number of successful pairs is greater than 0.5.

On a laundry drying line \(n\) socks hang in a random order (the order in which they got out of the washing machine). Among them there are the two favourite socks of the Scattered Scientist. The socks are covered by a drying sheet, so the Scientist does not see them, and takes out one sock by touch. Find the mathematical expectation of the number of socks taken out by the Scientist by the time he has both of his favourite socks.

\(N\) pairs of socks hang on a washing line in a random order (the order in which they were taken out of the washing machine). There are no two identical pairs. The socks hang under the drying sheet, so the Scattered Scientist takes out one toe by touch and compares each new sock with all of the previous ones. Find the mathematical expectation of the number of socks taken at the moment when the Scientist will have some pair.

In the cabinet of Anchuria there are 100 ministers. Among them there are honest and dishonest ministers. It is known that out of any ten ministers, at least one minister is dishonest. What is the smallest number of dishonest ministers there could be in the cabinet?

An ant goes out of the origin along a line and makes \(a\) steps of one unit to the right, \(b\) steps of one unit to the left in some order, where \(a > b\). The wandering span of the ant is the difference between the largest and smallest coordinates of the ant for the entire length of its journey.

a) Find the largest possible wandering range.

b) Find the smallest possible range.

c) How many different sequences of motion of the ant are there, where the wandering range is the greatest possible?

A square is divided into triangles (see the figure). How many ways are there to paint exactly one third of the square? Small triangles cannot be painted partially.

We will assume that the birth of a girl and a boy is equally probable. It is known that in some family there are two children.

a) What is the probability that one of them is a boy and one a girl?

b) Additionally, it is known that one of the children is a boy. What is the probability that there is one boy and one girl in the family now?

c) Additionally, it is known that the boy was born on a Monday. What is the probability that there is one boy and one girl in the family now?

The figure shows a payment order to pay an electricity bill to some power supply company for March 2013.

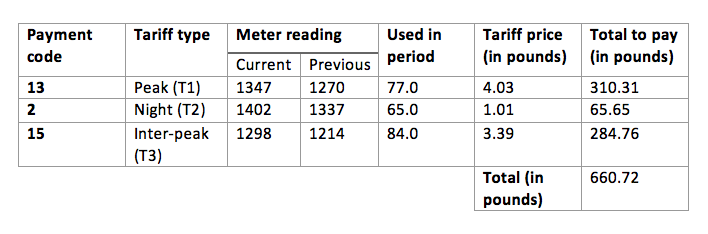
Every month, the client sends the company the testimony of a three-tariff meter installed her the apartment. From the indications for the current month, the corresponding indications for the previous month are subtracted, and the actual monthly expenditure is obtained for each of the three tariff zones (peak, night, inter-peak). Then the expense for each zone is multiplied by the price of one kilowatt-hour in this zone. Adding the received amounts, the client receives the total amount of payment for a month. In this example, the customer will pay £660.72.

The company maintains a record of electricity consumption and payment, using the data received from the customer. The problem is that the company sometimes confuses the six numbers obtained, rearranging them in an arbitrary order, however, it ensures that the current reading remains greater than the previous one. As a result, the calculation of the company may be flawed. If the company believes that the client must pay more than she has paid, the company requires additional payment.

Using the data from the receipt shown, find:

a) the maximum possible amount of surcharge for March 2013, which the company will require from the client;

b) the mathematical expectation of the difference between the amount that the company calculates and the amount paid by the client.