Problems

For a natural number \(n\) consider a regular \(2n\)-gon, with every vertex coloured either blue or green. It is known that the number of blue vertices equals the number of green vertices. Show that the number of main diagonals (passing through the centre of the \(2n\)-gon) with both ends blue is the same as the number of main diagonals with both ends green.

Jess and Tess are playing a game colouring points on a blank plane. Jess is moving first, she picks a non-colored point on a plane and colours it red. Then Tess makes a move, she picks \(2022\) colourless points on the plane and colours them all green. Jess then moves again, and they take turns. Jess wins if she manages to create a red equilateral triangle on the plane, Tess is trying to prevent that from happening. Will Jess always eventually win?

Can you cover a \(10 \times 10\) board using only \(T\)-shaped tetrominos?

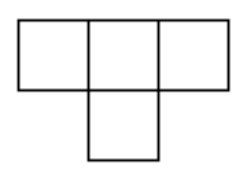
Can you cover a \(10 \times 10\) square with \(1 \times 4\) rectangles?

Two opposite corners were removed from an \(8 \times 8\) chessboard. Is it possible to cover this chessboard with \(1 \times 2\) rectangular blocks?

One unit square of a \(10 \times 10\) square board was removed. Is it possible to cover the rest of it with \(3\)-square \(L\)-shaped blocks?

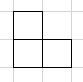
A \(7 \times 7\) square was tiled using \(1 \times 3\) rectangular blocks in such a way that one of the squares has not been covered. Find all the squares that could be left without being covered.

Can you cover a \(13 \times 13\) square using \(2 \times 2\) and \(3 \times 3\) squares?

Is it possible to cover a \(10 \times 10\) board with the \(L\)-tetraminos without overlapping? The pieces can be flipped and turned.

Coloring is a very neat technique in problems involving boards since it allows us to simplify the problem a great deal. The important part is focusing on an adequate subset of the squares, however doing it with colors is a lot easier.
The kinds of colorings can be very different and there is no general rule for determining which one is going to solve the problem. There are some colorings (such as a chessboard coloring) that are frequently used, but the only way to learn how to use this technique is by solving several problems of this style.
When the problem is related to pieces covering a certain figure, the “good colorings” are those that yield an invariant associated with the pieces. This can be the number of squares of one color they cover, the number of colors they may use, some parity argument, etc. Coloring is basically an illustrative way to describe invariants.