Problems

In a box there are \(20\) cards of blue, red, and yellow colours. Yellow cards outnumber red ones and there are six times less blue cards than yellow ones. What is the minimum number of cards that need to be drawn from the box without looking, to guarantee a red card among them?

There are two piles of rocks, \(10\) rocks in each pile. Fred and George play a game, taking the rocks away. They are allowed to take any number of rocks only from one pile per turn. The one who has nothing to take loses. If Fred starts, who has the winning strategy?

A group of \(15\) elves decided to pay a visit to their relatives in a distant village. They have a horse carriage that fits only \(5\) elves. In how many ways can they assemble the ambassador team, if at least one person in the team needs to be able to operate the carriage, and only \(5\) elves in the group can do that?

There are \(5\) pirates and they want to share \(8\) identical gold coins. In how many ways can they do it if each pirate has to get at least one coin?

Is \(100! = 100\times 99 \times ...\times 2\) divisible by \(2^{100}\)?

It is known that \(a + b + c = 5\) and \(ab + bc + ac = 5\). What are the possible values of \(a^2 + b^2 + c^2\)?

Prove the magic trick for the number \(1089 = 33^2\): if you take any \(3\)-digit number \(\overline{abc}\) with digits coming in strictly descending order and subtract from it the number obtained by reversing the digits of the original number \(\overline{abc} - \overline{cba}\) you get another \(3\)-digit number, call it \(\overline{xyz}\). Then, no matter which number you started with, the sum \(\overline{xyz} + \overline{zyx} = 1089\).
Recall that a number \(\overline{abc}\) is divisible by \(11\) if and only if \(a-b+c\) also is.

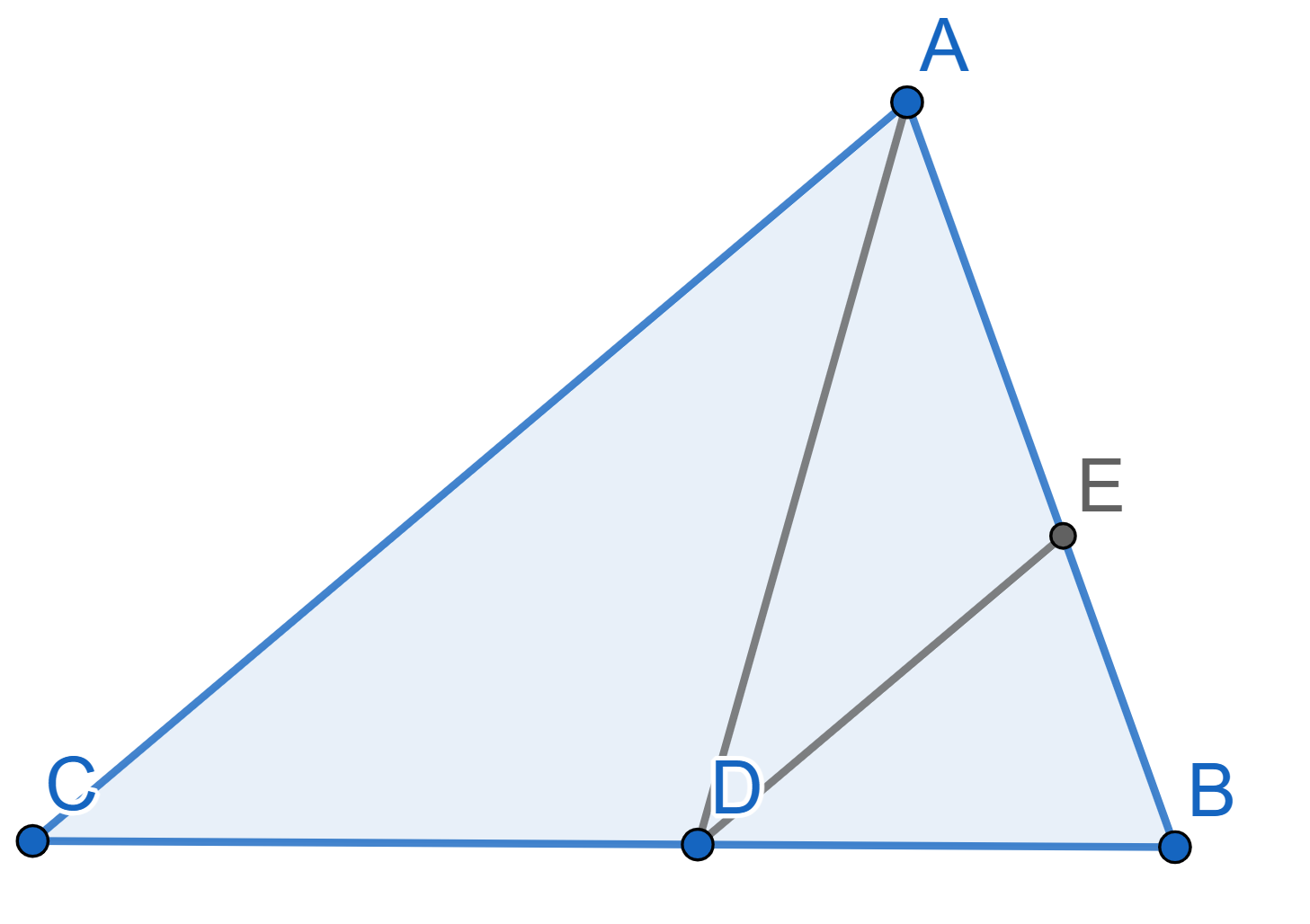
On the diagram below \(AD\) is the bisector of the triangle \(ABC\). The point \(E\) lies on the side \(AB\), with \(AE = ED\). Prove that the lines \(AC\) and \(DE\) are parallel.

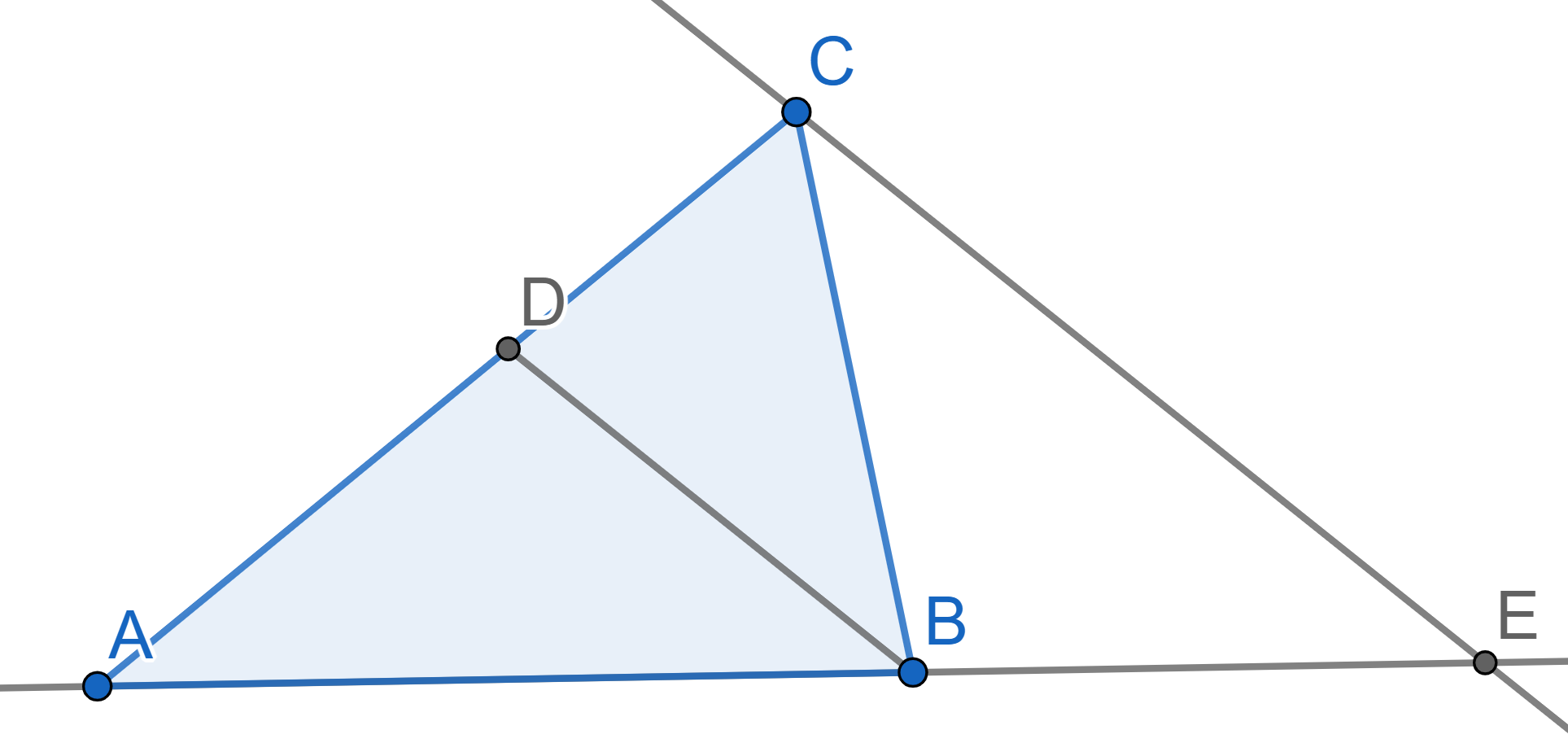
On the diagram below the line \(BD\) is the bisector of the angle \(\angle ABC\) in the triangle \(ABC\). A line through the vertex \(C\) parallel to the line \(BD\) intersects the continuation of the side \(AB\) at the point \(E\). Find the angles of the triangle \(BCE\) triangle if \(\angle ABC = 110^{\circ}\).

We want to wrap \(12\) Christmas presents in different coloured paper. We have \(6\) different patterns of paper and we want to use each one exactly twice. In how many ways can we do this?