Problems
Let’s prove that \(1\) is the smallest positive real number: Assume the contrary and let \(x\) be the smallest positive real number. If \(x>1\) then \(1\) is smaller, thus \(x\) is not the smallest. If \(x<1,\) then \(\frac{x}{2}<x\) so \(x\) can not be the smallest either. Then \(x\) can only be equal to \(1\).
Nick has written in some order all the numbers \(1,2,...33\) at the vertices of a regular \(33\)-gon. His little sister Hannah assigned to each side of the \(33\)-gon the number equal to the sum of the numbers at the ends of that side. It turns out that Hannah obtained \(33\) consecutive numbers in certain order. Can you find an arrangement of numbers as written by Nick which lead to this situation?
Is it possible to arrange the numbers \(1,\, 2,\, ...,\, 50\) at the vertices and middles of the sides of a regular \(25\)-gon so that the sum of the three numbers at the ends and in the middle of each side is the same for all sides?
Draw a shape that can be cut into \(4\) copies of the figure on the left or
into \(5\) copies of the figure on the
right (the figures can be rotated).
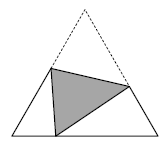
A equilateral triangle made of paper bends in a straight line so that
one of the vertices falls on the opposite side as shown on the picture.
Show that the corresponding angles of the two white triangles are
equal.
Sometimes proof of a statement requires elaborate reasoning, but sometimes it enough to provide an example when the described construction works. Often enough the problem is asking whether an event is possible, or if an object exists under certain conditions making the existence seemingly unlikely, in such cases all you need to do is to provide an example to solve the problem. Today we will see how to construct such examples.
In how many ways can you read the word TRAIN from the picture below, starting from T and going either down or right at each step?

There are \(100\) people in a room. Each person knows at least \(67\) others. Show that there is a group of four people in this room that all know each other. We assume that if person \(A\) knows person \(B\) then person \(B\) also knows person \(A\).
The numbers \(a\) and \(b\) are integers and the number \(p \ge 3\) is prime. Suppose that \(a+b\) and \(a^2 +b^2\) are divisible by \(p\). Show that \(a^2 + b^2\) is divisible by \(p^2\).
There are \(33\) cities in the Republic of Farfarawayland. The delegation of senators wants to pick a new capital city. They want this city to be connected by roads to every other city in the Republic. They know for a fact that given any set of \(16\) cities, there will always be some city that is connected by roads to all those selected cities. Show that there exists a suitable candidate for the capital.