Problems

Is it possible to cover a \(6 \times 6\) board with the \(L\)-tetraminos without overlapping? The pieces can be flipped and turned.

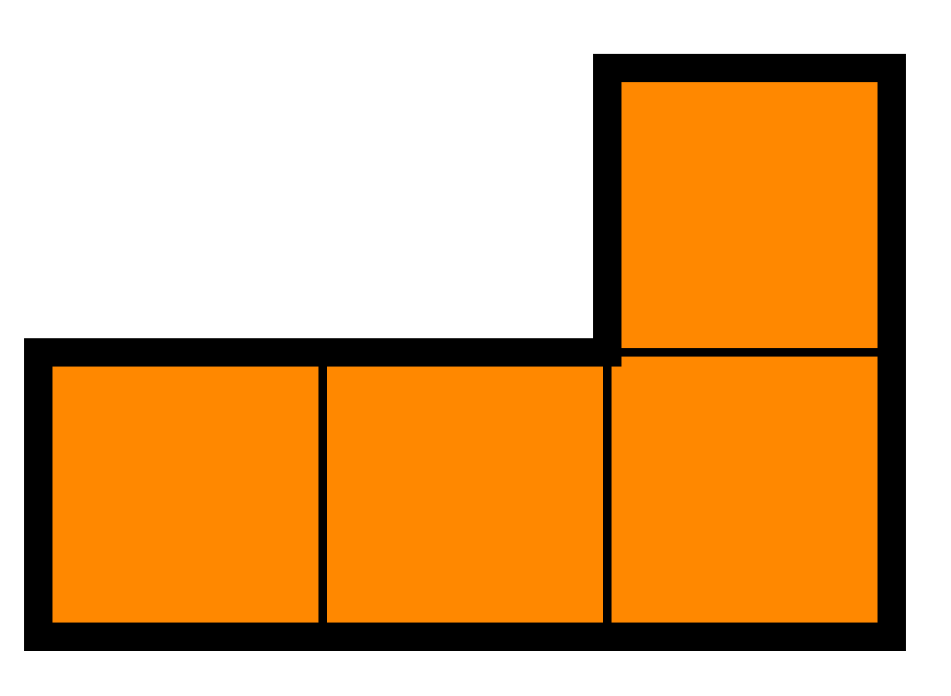
Is it possible to cover a \((4n+2) \times (4n+2)\) board with the \(L\)-tetraminos without overlapping for any \(n\)? The pieces can be flipped and turned.

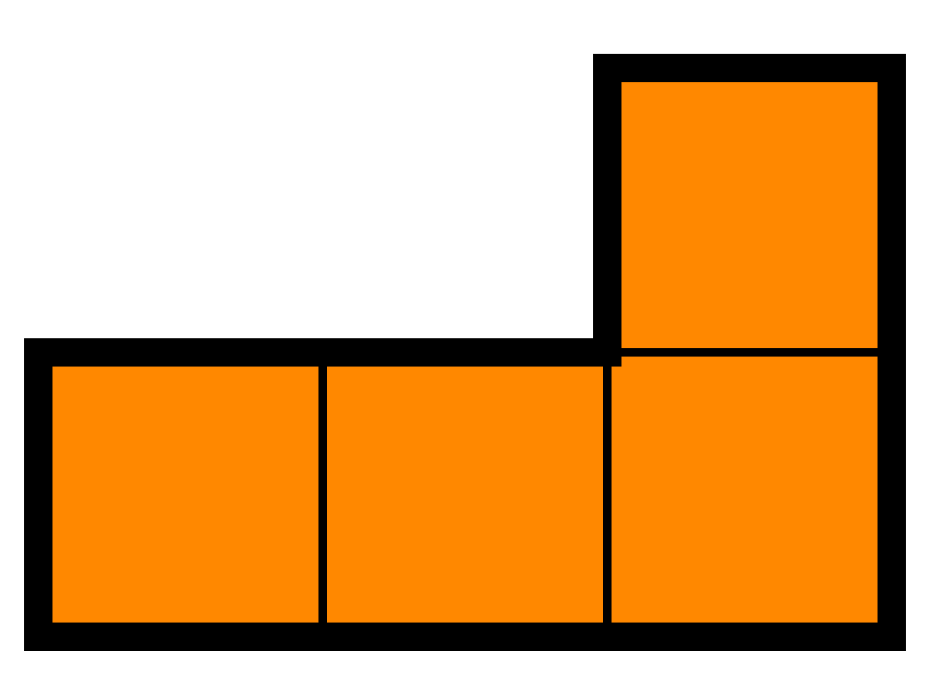
Is it possible to cover a \(4n \times 4n\) board with the \(L\)-tetraminos without overlapping for any \(n\)? The pieces can be flipped and turned.

There are \(100\) people standing in line, and one of them is Arthur. Everyone in the line is either a knight, who always tells the truth, or a liar who always lies. Everyone except Arthur said, "There are exactly two liars between Arthur and me." How many liars are there in this line, if it is known that Arthur is a knight?

Draw how Robinson Crusoe should use pegs, ropes, and sliding rings to tie his goat in order for the goat to graze grass in the shape of a square.

Draw how Robinson Crusoe should put pegs and ropes to tie his goat in order for the goat to graze grass in the shape of a parallelogram.

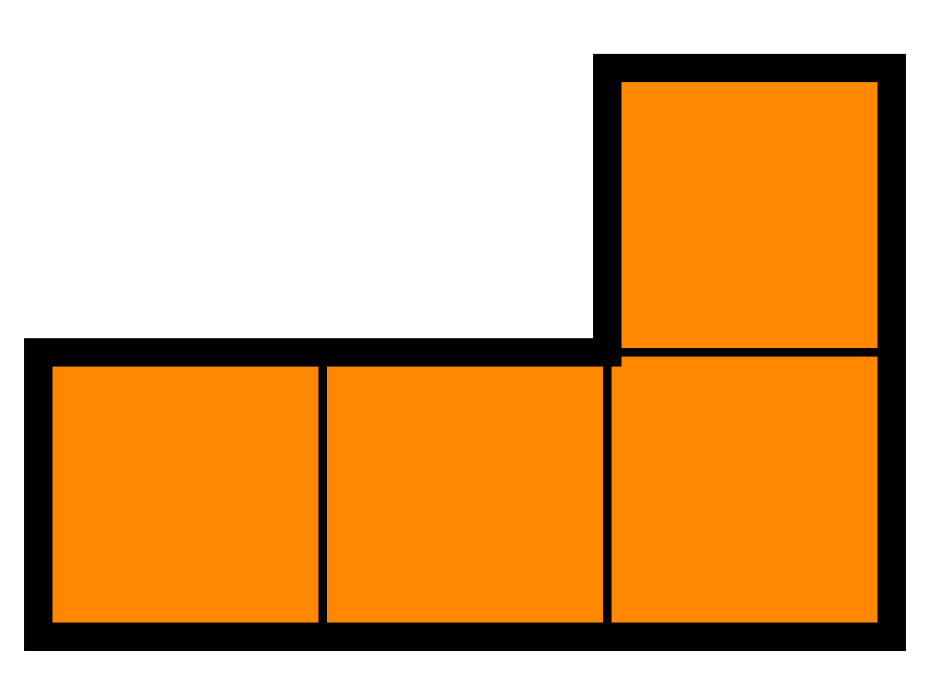
Draw how Robinson Crusoe should put pegs and ropes to tie his goat in order for the goat to graze grass in an area of the following shape:

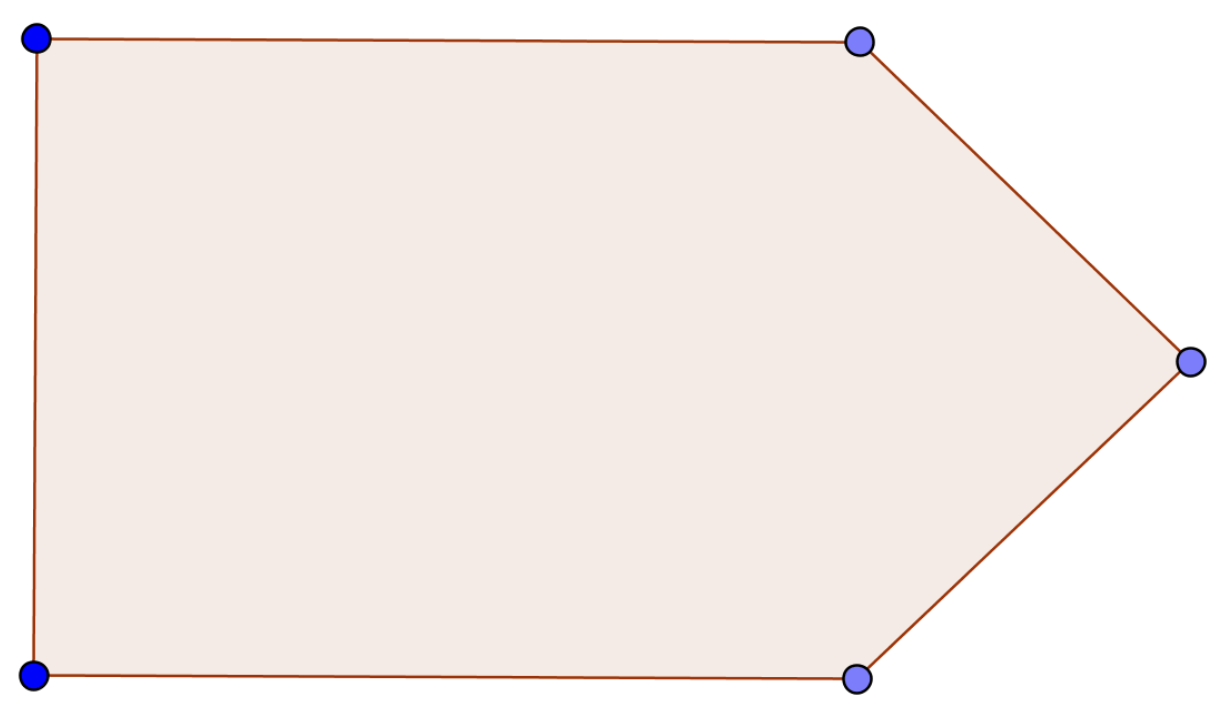
Draw how Robinson Crusoe should put pegs and ropes to tie his goat in order for the goat to graze grass in the shape of a given triangle.

Draw how Robinson Crusoe should arrange pegs and ropes so that his goat grazes in the shape of a hexagon. The hexagon doesn’t need to be regular.

Robinson Crusoe’s goat is tied to a single peg with one rope. Draw how Robinson should arrange pegs, ropes, a sliding ring, and a wolf so that the goat grazes in the shape of a half-circle.