Problems

A rook in chess can move any number of squares in the same row or column. Let’s invent a new figure, a "little rook" that can only move one square in each of these directions. If we start with the "little rook" in the bottom right corner of an $8\times 8$ chessboard, can we make it to the top left corner while visiting each square exactly once?

There are $15$ lightbulbs in a row, all switched off. We can pick any three of them and change their state. Can we repeat this operation an even number of times such that at the end all the lightbulbs are on?

There are numbers $1,2,3,4,5,6,7,8,9$ and $10$ written on a board. Each time you make a "move" you can erase three of the remaining numbers, $a,b$ and $c$, and replace them with the numbers $2a+b,2b+c$ and $2c+a$. Is it possible to make all the $10$ numbers left on the board equal?

On a certain island there are $17$ grey, $15$ brown and $13$ crimson chameleons. If two chameleons of different colours meet, both of them change to the third colour. No other colour changes are allowed. Is it possible that after a few such colour transitions all the chameleons have the same colour?

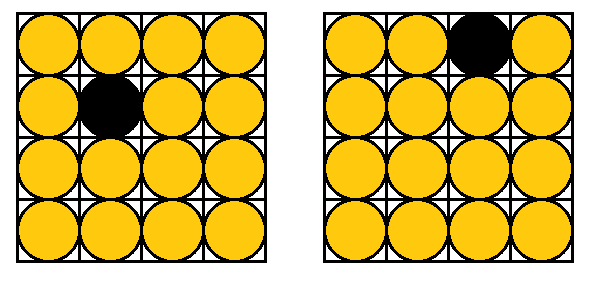
Sixteen lightbulbs are arranged in a $4\times 4$ grid. Some of them are on, the other ones are off. You are allowed to change the state of all the bulbs in a column, in a row, or along any diagonal (note: there are $14$ diagonals in total!). Is it possible to go from the arrangement on the left to the one on the right by repeating this operation?

The numbers $1$ to $2025$ are written on a board. In one move we can erase two numbers and replace them with the absolute value of their difference. Can we achieve a sequence consisting of only $0$ after some number of moves?

Sometimes a problem describes a certain process and asks you whether a certain result can be achieved through a series of repeated actions. How could we prove that such a result is impossible to obtain? One of the ways is to observe all the properties of the process that do not change after performing some action, or alternatively, properties that change in a predictable way. We call these properties "Invariants".

Hard. Let $\mathcal{S}$ be a finite set of at least two points in the plane. Assume that no three points of $\mathcal{S}$ are collinear. A windmill is a process that starts with a line $\ell$ going through a single point $P\in \mathcal{S}$. The line rotates clockwise about the pivot $P$ until the first time that the line meets some other point belonging to $\mathcal{S}$. This point, $Q$, takes over as the new pivot, and the line now rotates clockwise about $Q$, until it next meets a point of $\mathcal{S}$. This process continues indefinitely. Show that we can choose a point $P$ in $\mathcal{S}$ and a line $\ell$ going through $P$ such that the resulting windmill uses each point of $\mathcal{S}$ as a pivot infinitely many times.

In the quadrilateral $ABCD$ the diagonals $AC$ and $BD$ intersect at the point $E$. It is known that the perimeter of the triangle $ABC$ is equal to the perimeter of the triangle $ABD$, and the perimeter of the triangle $ACD$ equals the perimeter of the triangle $BCD$.

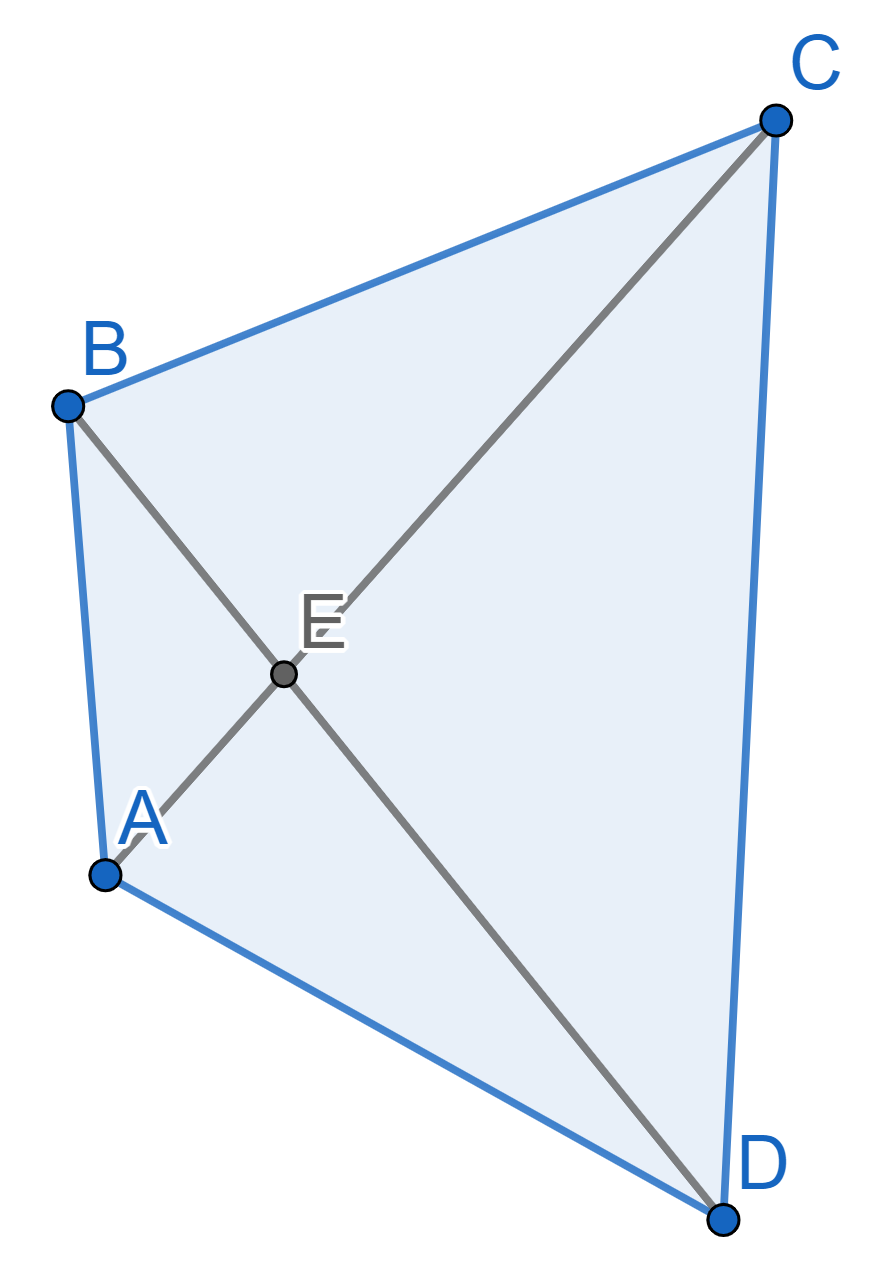
Prove that $AE=BE$.

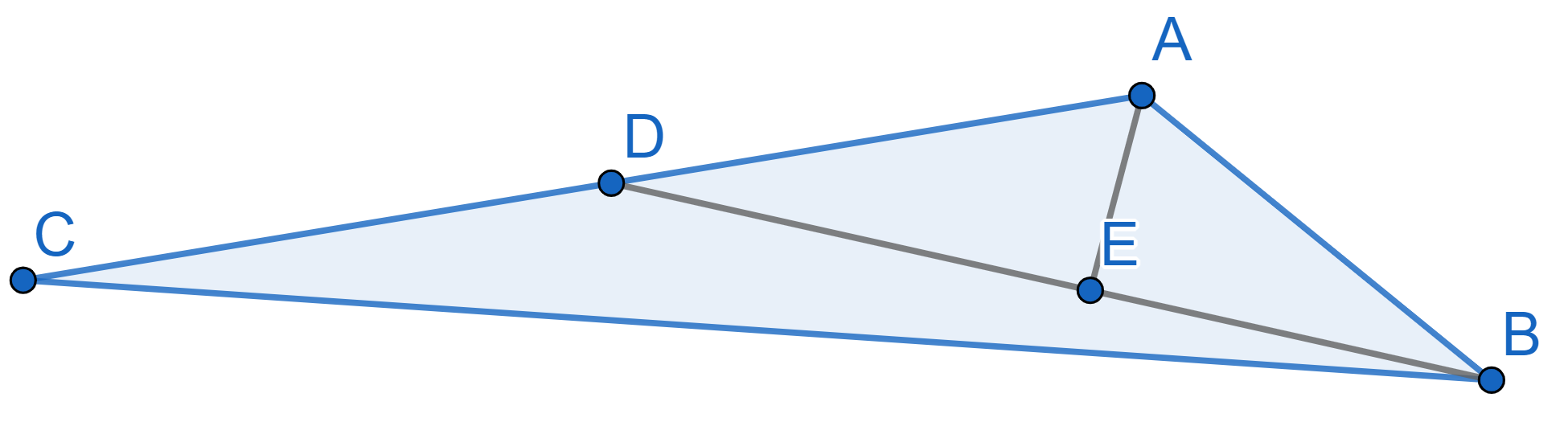
In the triangle $ABC$ the segment $AB=5$ and the segment $BD$ is the median. The segment $AE$ is perpendicular to $BD$ and divides $BD$ in half. Find the length of $AC$.