Problems
Prove for any natural number \(n\) that \((n + 1)(n + 2). . .(2n)\) is divisible by \(2^n\).
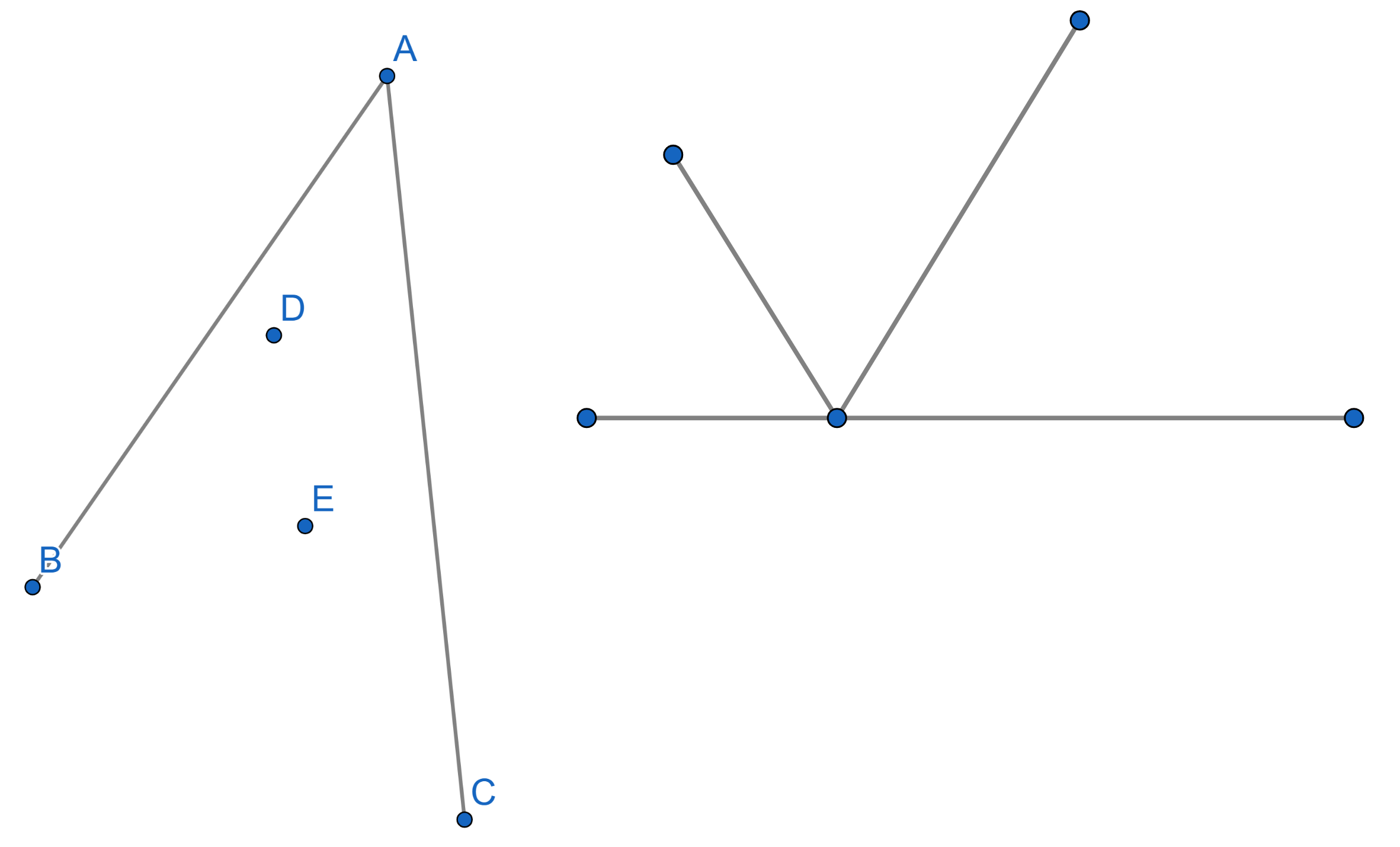
Between two mirrors \(AB\) and \(AC\), forming a sharp angle two points
\(D\) and \(E\) are located. In what direction should
one shine a ray of light from the point \(D\) in such a way that it would reflect off
both mirrors and hit the point \(E\)?
If a ray of light comes towards a surface under a certain angle, it is
reflected with the same angle as on the picture.
Consider a set of natural numbers \(A\), consisting of all numbers divisible by \(6\), let \(B\) be the set of all natural numbers divisible by \(8\), and \(C\) be the set of all natural numbers divisible by \(12\). Describe the sets \(A\cup B\), \(A\cup B\cup C\), \(A\cap B\cap C\), \(A-(B\cap C)\).
Let \(a\), \(b\) and \(c\) be the three side lengths of a triangle. Does there exist a triangle with side lengths \(a+1\), \(b+1\) and \(c+1\)? Does it depend on what \(a\), \(b\) and \(c\) are?
There is a triangle with side lengths \(a\), \(b\)
and \(c\). Can you form a triangle with
side lengths \(\frac{a}{b}\), \(\frac{b}{c}\) and \(\frac{c}{a}\)? Does it depend on what \(a\), \(b\)
and \(c\) are? Give a proof if it is
always possible or never possible. Otherwise, construct examples to show
the dependence on \(a\), \(b\) and \(c\).
Recall that a triangle can be drawn with side lengths \(x\), \(y\)
and \(z\) if and only if \(x+y>z\), \(y+z>x\) and \(z+x>y\).
There is a triangle with side lengths \(a\), \(b\)
and \(c\). Does there exist a triangle
with side lengths \(|a-b|\), \(|b-c|\) and \(|c-a|\)? Does it depend on what \(a\), \(b\)
and \(c\) are?
Recall that a triangle can be formed with side lengths \(x\), \(y\)
and \(z\) if and only if all the
inequalities \(x+y>z\), \(y+z>x\) and \(z+x>y\) hold.
There is a triangle with side lenghts \(a\), \(b\) and \(c\). Does there exist a triangle with sides of lengths \(a^2+bc\), \(b^2+ca\) and \(c^2+ab\)? Does it depend on the values of \(a\), \(b\) and \(c\)?
In good conditions, bacteria in a Petri cup spread quite fast, doubling every second. If there was initially one bacterium, then in \(32\) seconds the bacteria will cover the whole surface of the cup.
Now suppose that there are initially \(4\) bacteria. At what time will the bacteria cover the surface of the cup?
A piece containing exactly \(4\) black cells is cut out from a regular \(8\) by \(8\) chessboard. You are only allowed to cut along the edges of the cells and the piece must be connected - namely you cannot have cells attached only with a vertex, they have to share a common edge.
Find the largest possible area of such a piece.
Prove that the set of all finite subsets of natural numbers \(\mathbb{N}\) is countable. Then prove that the set of all subsets of natural numbers is not countable.