Problems
a) Can you measure \(5\) litres of
milk using two buckets of volumes \(4\)
and \(11\) litres respectively?
b) Can you measure \(7\) litres of milk
using buckets of volumes \(8\) and
\(12\) litres respectively?
a) A mighty dragon has several rubies in his treasure. He is able to
divide the rubies into groups of \(3\),
\(5\) or \(11\). How many rubies does he have, if we
know that is fewer than \(200\)?
b) The same dragon also has some emeralds. He is \(6\) emeralds short to be able to divide
them into groups of \(13\), one emerald
short to be able to divide them into groups of \(5\), but if he wants to divide them into
groups of \(8\), he is left with one
emerald. How many emeralds does he have if we know it is fewer than
\(500\)?
Let \(n\) be a natural number. Show that the fraction \(\frac{21n+4}{14n+3}\) is irreducible, i.e. it cannot be simplified.
Let \(m\) and \(n\) be two positive integers with \(m<n\) such that \[\gcd(m,n)+ \text{lcm}(m,n)=m+n.\] Show that \(m\) divides \(n\).
The numbers \(x,a,b\) are natural. Show that \(\gcd(x^a -1,x^b-1) = x^{\gcd(a,b)}-1\).
Let \(p\) be a prime number bigger than \(3\). Prove that \(p^2-1\) is a multiple of 24.
Is it possible to draw \(K_5\) without intersecting edges on a Möbius band? Recall that \(K_5\) is the complete graph on \(5\) vertices. That is, \(5\) points with an edge between every pair of different points.
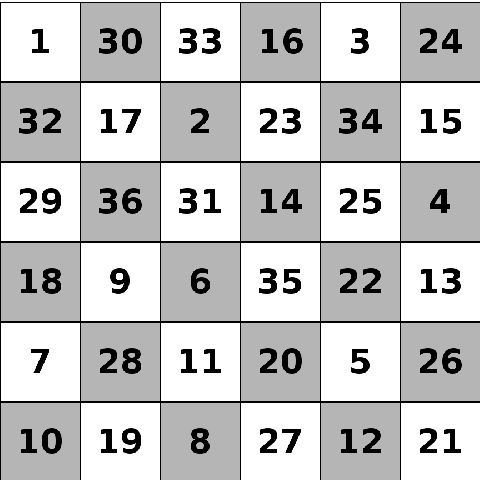
In chess, knights can move one square in one direction and two squares in a perpendicular direction. This is often seen as an ‘L’ shape on a regular chessboard. A closed knight’s tour is a path where the knight visits every square on the board exactly once, and can get to the first square from the last square.
This is a closed knight’s tour on a \(6\times6\) chessboard.
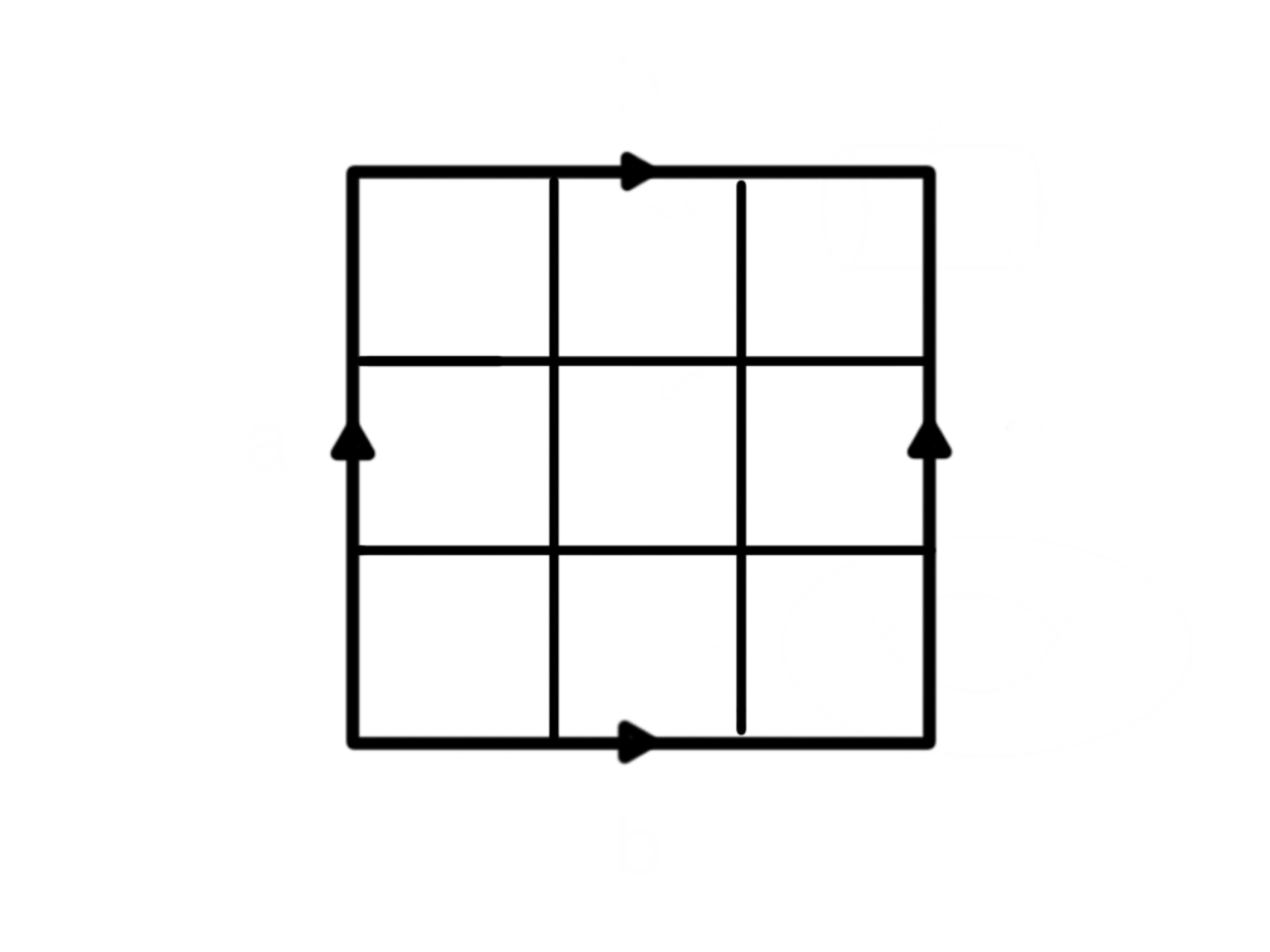
Can you draw a closed knight’s tour on a \(3\times3\) torus? That is, a \(3\times3\) square with both pairs of opposite sides identified in the same direction, like the diagram below.
You may remember the game Nim. We will now play a slightly modified version, called Thrim. In Thrim, there are two piles of stones (or any objects of your choosing), one of size \(1\) and the other of size \(5\). Whoever takes the last stone wins. The players take turns to remove stones - they can only remove stones from one pile at a time, and they can remove at most \(3\) stones at a time. Does the player going first or the player going second have a winning strategy?
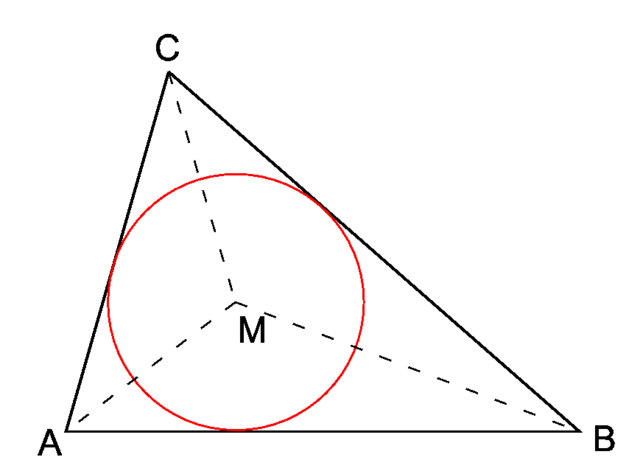
A circle is inscribed in a triangle (that is, the circle touches the sides of the triangle on the inside). Let the radius of the circle be \(r\) and the perimeter of the triangle be \(p\). Prove that the area of the triangle is \(\frac{pr}{2}\).