Problems
In a graph \(G\), we call a
matching any choice of edges in \(G\) in such a way that all vertices have
only one edge among chosen connected to them. A perfect
matching is a matching which is arranged on all vertices of the
graph.
Let \(G\) be a graph with \(2n\) vertices and all the vertices have
degree at least \(n\) (the number of
edges exiting the vertex). Prove that one can choose a perfect matching
in \(G\).
Imagine you are a manager of a very special hotel, a hotel with an
infinite number of rooms, where each room has a natural number on the
door \(1,2,3,4,...\). Only one guest
can stay in each room and in most cases the hotel will be initially full
with no vacant rooms left.
You will have to deal with unusual situations that may occur.
A new customer comes to the hotel and wants a room. It happened today that all the rooms are occupied. What should you do?

Now imagine you got \(10\) new guests arriving to the completely full hotel. What should you do now?
The next day you have even harder situation: to the hotel, where all the rooms are occupied arrives a bus with infinitely many new customers. In the bus all the seats have numbers \(1,2,3...\) corresponding to all natural numbers. How to deal with this one?
Imagine you have \(2\) new guests arriving to the full hotel. How do you accommodate them?
What would you do about \(10000\) new guests arriving to the full hotel?
Imagine you have now a general finite number of new guests arriving to the full hotel. What do you do?
Today we will solve some geometric problems using the triangle inequality. This is an inequality between the lengths of the sides of any triangle, or between the distances of any three points.
The shortest path between any two points \(A\) and \(B\) is a straight segment - every other path is longer. In particular, a path through another point, \(C\), is equal or longer. \[AC + BC \ge AB\] The triangle inequality says that the sum of lengths of any two sides of a triangle is always larger than the length of the third side. The inequality only becomes an equality if \(ABC\) is not actually a triangle and the point \(C\) lies on the segment from \(A\) to \(B\).
Even though it is a simple idea, it can be a really helpful tool in problem solving.
A set is a collection of objects of any specified kind, the objects
are called elements or members, the objects in one set cannot repeat,
namely \(\{1,2,3\}\) and \(\{1,2,2,2,3\}\) are identical sets. We
denote a set by a capital letter \(A\),
or \(B\) and write \(x\in A\) if \(x\) is an element of \(A\), and \(x\notin A\) if it is not. The notation
\(A=\{a,b,c,...\}\) means that the set
\(A\) consists of the elements \(a,b,c,...\). The empty or void set, \(\emptyset\), has no elements. If all
elements of \(A\) are also in \(B\), then we call \(A\) a subset of \(B\) and we write \(A\subseteq B\). It is an axiom that the
sets \(A\) and \(B\) are equal \(A=B\) if they have the same elements.
Namely, \(A\) is a subset of \(B\) and \(B\) is a subset of \(A\) at the same time.
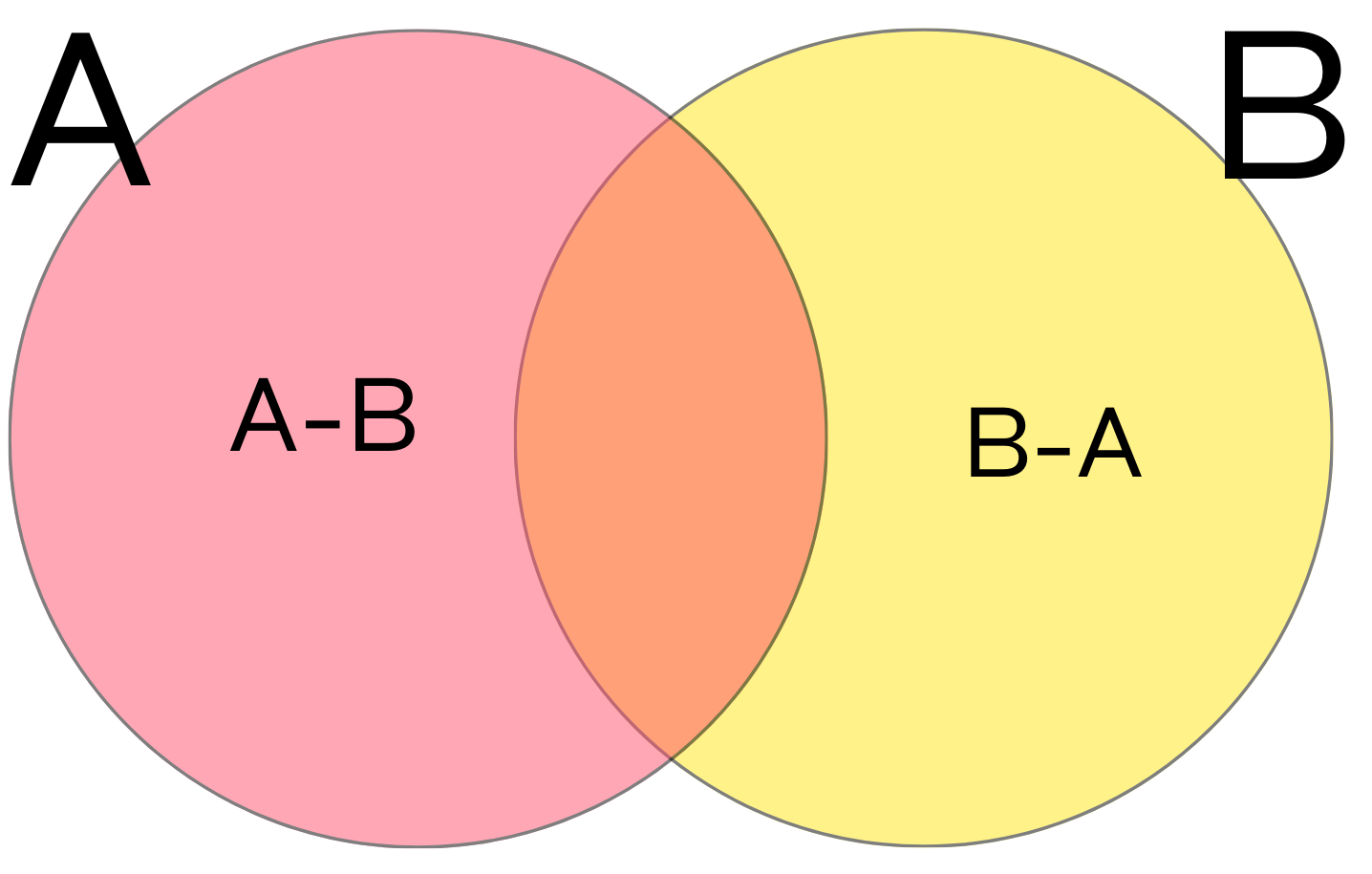
For any sets \(A\) and \(B\), we define their union \(A\cup B\), intersection \(A\cap B\), and the difference \(A-B\) as follows:
the union \(A\cup B\) is the set of all elements that belong to \(A\) or \(B\);
the intersection \(A\cap B\) is the set of elements that belong to both \(A\) and \(B\);
the difference \(A-B\) consists of those \(x \in A\) that are do not belong to \(B\).
Sometimes it is useful to draw sets as Venn diagrams, on the diagram below the pink circle represents the set \(A\), the yellow circle represents the set \(B\), the orange part is the intersection \(A\cap B\), the pink part is \(A-B\), the yellow part is \(B-A\), and the whole picture is the union \(A\cup B\).