Problems
Among the first \(20\) Fibonacci numbers: \(F_0 = 0,F_1 = 1,F_2 = 1, F_3 = 2, F_4 = 3,..., F_{20} = 6765\) check whether the numbers with prime index are prime. The index is another name for a number’s place in the sequence.
Consider Pascal’s triangle: it starts with \(1\), then each entry in the triangle is the sum of the two numbers above it. Prove that the diagonals of Pascal’s triangle add up to Fibonacci numbers.

Prove for any integers \(m,n\ge0\)
that \(F_{m+n} = F_{m-1}F_n +
F_mF_{n+1}\).
Corollary: if \(k\mid
n\), then \(F_k\mid F_n\). This
can be proven by induction if we write \(n=sk\) for a natural \(s\), then \[F_{k+(s-1)k} = F_{k-1}F_{(s-1)k} +
F_kF_{(s-1)k+1}.\]
Denote by \(\gcd(m,n)\) the greatest common divisor of numbers \(m,n\), namely the largest possible \(d\) which divides both \(n\) and \(m\). Prove for any \(m,n\) that \[\gcd(F_n,F_m) = F_{\gcd(m,n)}.\]
Suppose that \(p\) is a prime number. How many numbers are there less than \(p^2\) that are relatively prime to \(p^2\)?
How many cuboids are contained in an \(n\times n\times n\) cube? For example, we’ve got \(n^3\) cuboids of size \(1\times1\times1\), and obviously just \(1\) of size \(n\times n\times n\) (which is the whole cube itself). But we also have to count how many there of size \(1\times1\times2\), \(1\times2\times3\), and several more.
In the \(6\times7\) large rectangle shown below, how many rectangles are there in total formed by grid lines?

Simplify \(F_0-F_1+F_2-F_3+...-F_{2n-1}+F_{2n}\), where \(n\) is a positive integer.
Explain why a position \(g\) is a winning position if there is a move that turns \(g\) into a losing position. On the other hand, explain why a position is a losing position if all moves turns it into a winning position.
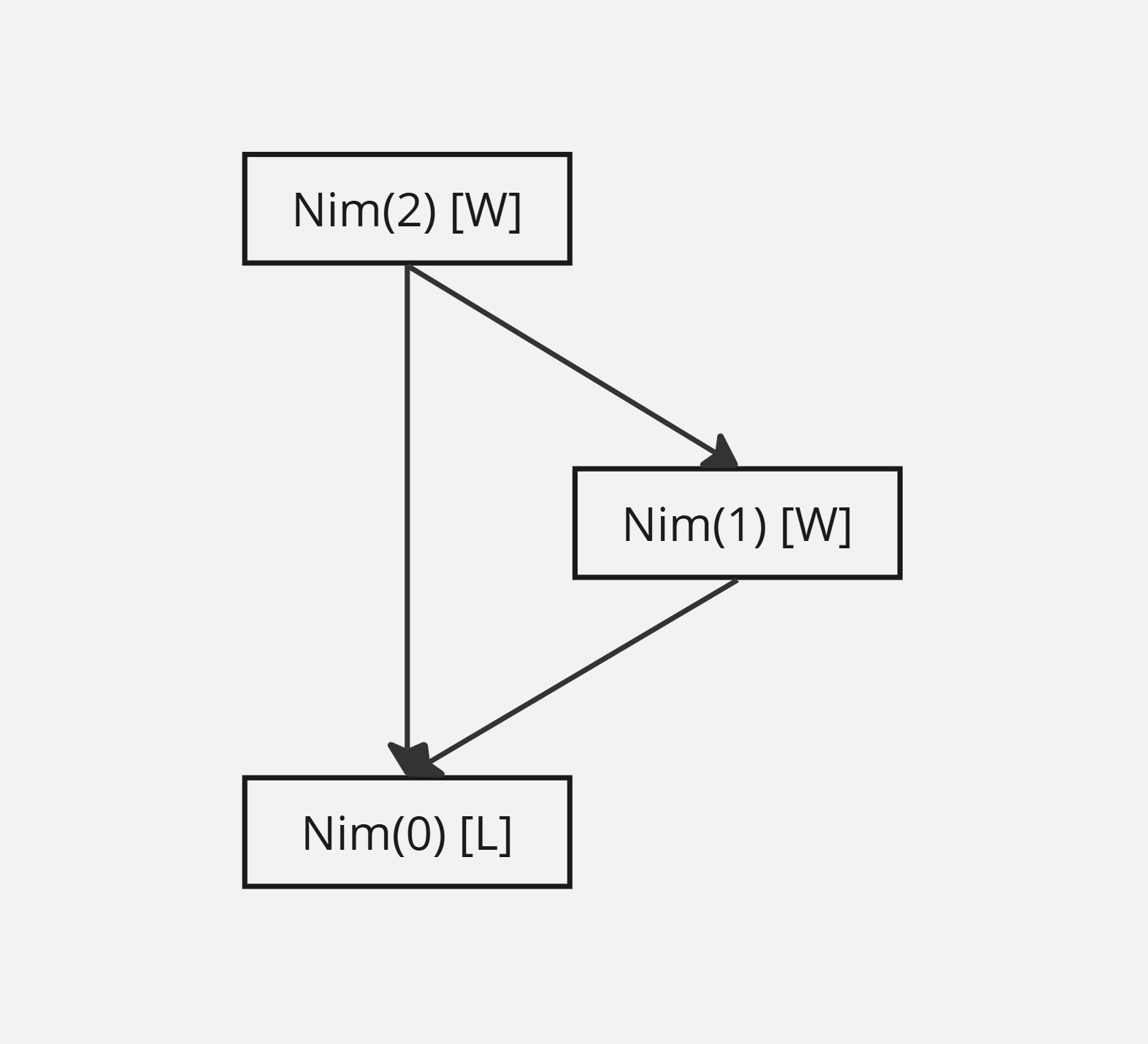
A technique that can be used to completely solve certain games is drawing game graphs. Given a game \(G\), we draw an arrow pointing from a position \(g\) to a position \(h\) if there is a move from \(g\) to \(h\).
As a simple example, the game graph of \(\text{Nim}(2)\) is shown below.
Draw the game graph of \(\text{Nim}(2,2)\). Is \(\text{Nim}(2,2)\) a winning position or losing position?