Problems
Find the minimal natural number \(n>1\) such that \(n^6 - 2n^5 - n^4 + 4n^3 - n^2 - 2n +1\) is divisible by \(2025\).
In chess, knights can move one square in one direction and two squares in a perpendicular direction. This is often seen as an ‘L’ shape on a regular chessboard. A closed knight’s tour is a path where the knight visits every square on the board exactly once, and can get to the first square from the last square.
This is a closed knight’s tour on a \(6\times6\) chessboard.
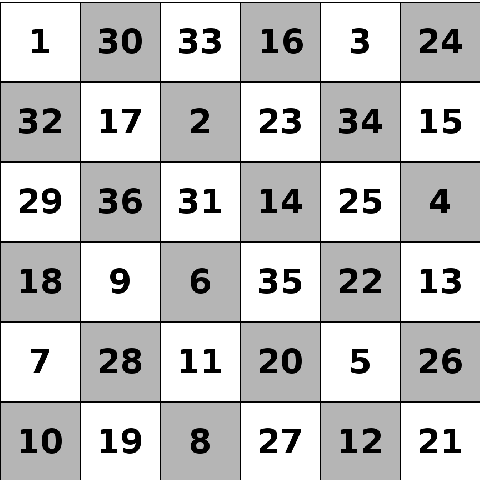
Can you draw a closed knight’s tour on a \(4\times4\) torus? That is, a \(4\times4\) square with both pairs of opposite sides identified in the same direction, like the diagram below.
Prove that one can tile the whole plane without spaces and overlaps, using any non self-intersecting quadrilaterals of the same shape. Note: quadrilaterals might not be convex.
Let \(n\) be a positive integer. We denote by \(s(n)\) the sum of the divisors of \(n\). For example, the divisors of \(n=6\) are \(1\), \(2\), \(3\) and \(6\), so \(s(6)=1+2+3+6=12\). Prove that, for all \(n\ge1\), \[\sum_{k=1}^ns(k)=s(1)+s(2)+...+s(n)\le\frac{\pi^2}{12}n^2+\frac{n\log n}{2}+\frac{n}{2}.\]
It is impossible to completely tile the plane using only regular pentagons. However, can you identify at least three different types of pentagons (each with at least two different corresponding sides AND angles) that can be used to tile the plane in three distinct ways? Here essentially different means the tilings have different patterns.
Draw how to tile the whole plane with figures, made from squares \(1\times 1\), \(2\times 2\), \(3\times 3\), where squares are used the same number of times in the design of the figure.
Consider a line segment of length \(3m\). Jack chose \(4\) random points on the segment and measured all the distances between those \(4\) points. Prove that at least one of the distances is less than or equal to \(1m\).
The kingdom of Triangland is an equilateral triangle of side \(10\) km. There are \(5\) cities in this kingdom. Show that some two of them are closer than \(5\) km apart.
Margaret marked three points with integer coordinates on a number line with a red crayon. Meanwhile Angelina marked the midpoint of each pair of red points with a blue crayon. Prove that at least one of the blue points has an integer coordinate.
Margaret and Angelina coloured points in the second dimension. Now Margaret marked five points with both integer coordinates on a plane with a red crayon, while Angelina marked the midpoint for each pair of red points with a blue crayon. Prove that at least one of the blue points has both integer coordinates.