Problems
It is impossible to completely tile the plane using only regular pentagons. However, can you identify at least three different types of pentagons (each with at least two different corresponding sides AND angles) that can be used to tile the plane in three distinct ways? Here essentially different means the tilings have different patterns.
Draw how to tile the whole plane with figures, made from squares \(1\times 1\), \(2\times 2\), \(3\times 3\), where squares are used the same number of times in the design of the figure.
Consider a line segment of length \(3m\). Jack chose \(4\) random points on the segment and measured all the distances between those \(4\) points. Prove that at least one of the distances is less than or equal to \(1m\).
The kingdom of Triangland is an equilateral triangle of side \(10\) km. There are \(5\) cities in this kingdom. Show that some two of them are closer than \(5\) km apart.
Margaret marked three points with integer coordinates on a number line with a red crayon. Meanwhile Angelina marked the midpoint of each pair of red points with a blue crayon. Prove that at least one of the blue points has an integer coordinate.
Margaret and Angelina coloured points in the second dimension. Now Margaret marked five points with both integer coordinates on a plane with a red crayon, while Angelina marked the midpoint for each pair of red points with a blue crayon. Prove that at least one of the blue points has both integer coordinates.
Anna has a garden of square shape with side \(4\) m. After playing with her dog in the garden she left \(5\) dog toys on the lawn. Show that some two of them are closer than \(3\) m apart.
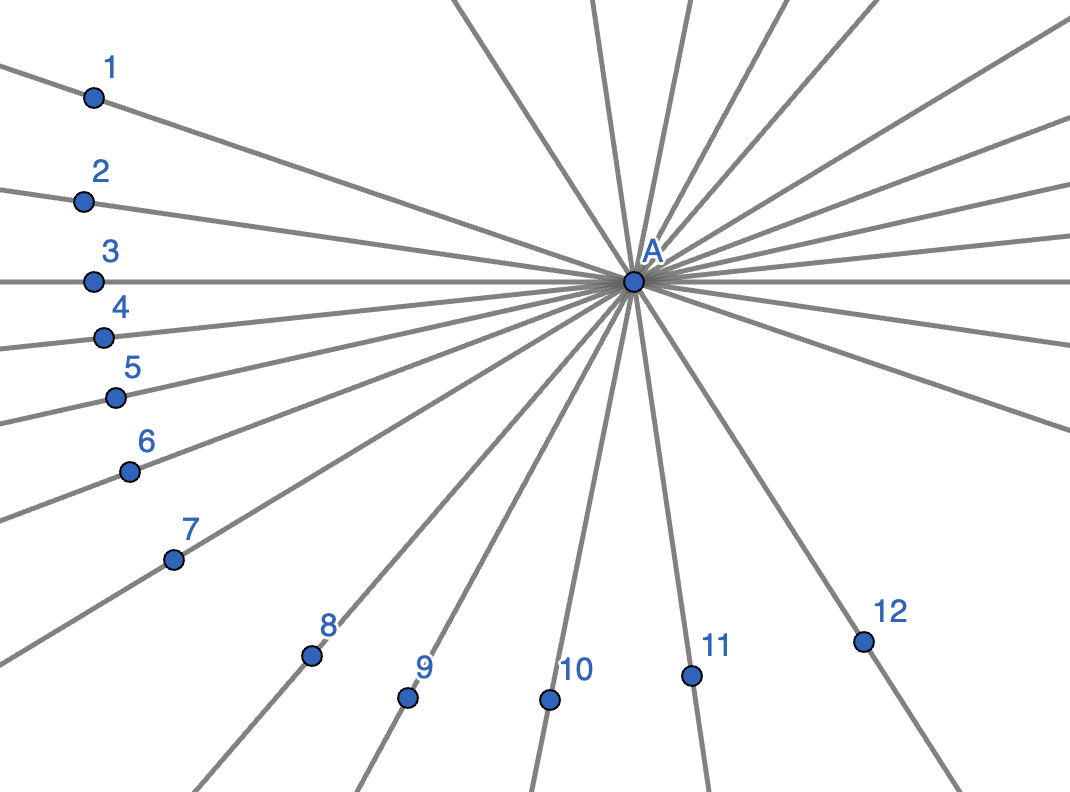
Twelve lines are drawn on the plane, passing through a point \(A\). Prove that there are two of them with angle less than \(17^{\circ}\) between them.
Inside a square of area \(6\), there are three polygons, each of area \(3\). Show that some two of these polygons overlap and the area of the overlap is at least \(1\).
A Wimbledon doubles court is \(78\)ft\(\times36\)ft. After a long practice match, there were \(79\) tennis balls in the court area. Show that some two of the balls were at most \(6\sqrt{2}\)ft away from each other.