Problems
Take a (finite) set \(S\), say \([n]\) and a random function \(f:S\to S\). What’s the distribution of the limiting size of the image of the iterates of \(f\)?
That is, \(\lim_{N\to\infty}|f^N([n])|\)
By random, let \(i\in[n]\). Each \(f(i)\) is independently and identically distributed as uniform random variables on \([n]\). One can also think of it as \(f\) is taken uniformly from the \(n^n\) possible functions \([n]\to[n]\).
Today we’ll look at 3-dimensional shapes, including their volumes and surfaces areas. One special kind are the Platonic Solids - the tetrahedron, cube, octahedron, dodecahedron and icosahedron.
In the picture below, there are the \(12\) pentominoes. Is it possible to tile a \(6\times10\) rectangle with them, using each pentominoe exactly once?
Show how to tile a \(5\times12\) rectangle with the twelve pentominoes.
Show how to tile a \(4\times15\) rectangle with the twelve pentominoes.
Is it possible to tile a \(3\times20\) rectangle with the twelve pentominoes?
How can we tile the plane with this cube net?
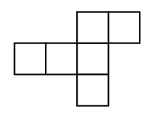
How can we tile the plane with this cube net?
Queen Hattius has two prisoners and gives them a puzzle. If they succeed, then she’ll let them free. She will randomly put a hat on each of their heads. The hats could be red or blue. They will simultaneously guess the colour of their own hat, and if at least one person is correct, then they win.
Each prisoner can only see the other prisoner’s hat - and not their own. The prisoners aren’t allowed to communicate once they’re wearing the hats, but they’re allowed to come up with a strategy before.
What should their strategy be?
Today we’ll look at various logic puzzles where you have to imagine what’s going on inside someone else’s head. What they’re thinking about could be about what’s going on inside your own head!