Problems

Four mice are chosen (without replacement) from a litter, two of which are white. The probability that both white mice are chosen is twice the probability that neither is chosen. How many mice are there in the litter?

A flea hops about at random on the vertices of a triangle where each hop is from the currently occupied vertex of one of the other two vertices each with probability \(\frac{1}{2}\). Find the probability that after \(n\) hops the flea is back where it started.

A city planning committee contains a proportion \(p\) of members of the Even party, who never change their minds about anything, and a proportion \(1-p\) of members of the Odd party who change their minds completely at random (with probability \(r\)) between successive votes on the same issue. A randomly chosen committee member is noticed to have voted twice in succession in the same way. What is the probability that this member will vote in the same way next time?

A bin has \(2\) white balls and \(3\) black balls. You play a game as follows: you draw balls one at a time without replacement. Every time you draw a white ball , you win a dollar, but every time you draw a black ball, you lose a dollar. You can stop the game at any time. Devise a strategy for playing this game which results in an expected profit.

Take a (finite) set \(S\), say \([n]\) and a random function \(f:S\to S\). What’s the distribution of the limiting size of the image of the iterates of \(f\)?

That is, \(\lim_{N\to\infty}|f^N([n])|\)

By random, let \(i\in[n]\). Each \(f(i)\) is independently and identically distributed as uniform random variables on \([n]\). One can also think of it as \(f\) is taken uniformly from the \(n^n\) possible functions \([n]\to[n]\).

Today we’ll look at 3-dimensional shapes, including their volumes and surfaces areas. One special kind are the Platonic Solids - the tetrahedron, cube, octahedron, dodecahedron and icosahedron.

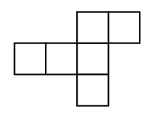
In the picture below, there are the \(12\) pentominoes. Is it possible to tile a \(6\times10\) rectangle with them?

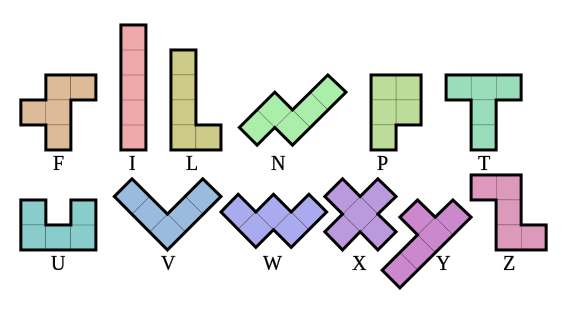
Show how to tile a \(5\times12\) rectangle with the twelve pentominoes.

Show how to tile a \(4\times15\) rectangle with the twelve pentominoes.

Is it possible to tile a \(3\times20\) rectangle with the twelve pentominoes?