Problems
Alice was playing on the \(5\times 5\) lights out board and obtained this light pattern:
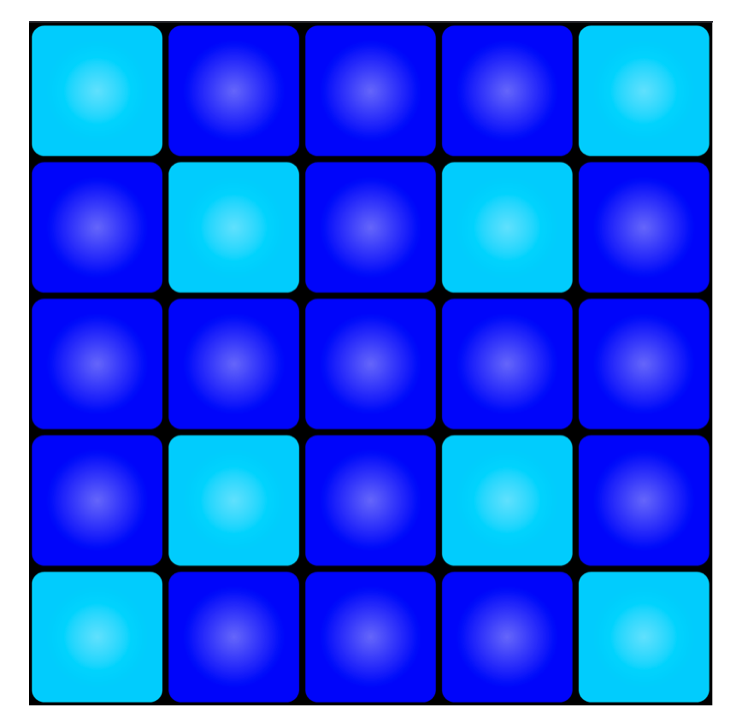
how did she obtain it?
After some playing with the \(3\times 3\) board, Sam guessed that there were \(900\) different light patterns that could be obtained by playing on this board. Was he right?
Suppose that \(x_1+y_1\sqrt{d}\) and \(x_2+y_2\sqrt{d}\) give solutions to Pell’s equation \(x^2-dy^2=1\) and \(x_1,x_2,y_1,y_2\geq 0\). Show that the following are equivalent:
\(x_1+y_1\sqrt{d} < x_2+y_2\sqrt{d}\),
\(x_1<x_2\) and \(y_1<y_2\),
\(x_1<x_2\) or \(y_1<y_2\).
If Pell’s equation \(x^2-dy^2 = 1\) has a nontrivial solution \((x_1,y_1)\), show that it has infinitely many distinct solutions.
Show that there are infinitely many triples of consecutive integers, each of which is a sum of the square of two integers.
Suppose that Pell’s equation \(x^2-dy^2=1\) has a solution \((x_1,y_1)\) where \(x_1,y_1\) are positive and \(y_1\) is minimal among all solutions with positive \(x,y\). Show that if \(x+y\sqrt{d}\) gives a solution to \(x^2-dy^2=1\), then \(x+y\sqrt{d}=\pm(x_1+y_1\sqrt{d})^k\) for some integer \(k\).
The original “Lights Out” game works like this: a light pattern is shown on the board, and your task is to turn all the lights off. A light pattern is called solvable if you can complete the game starting from that pattern. Ziheng and Jan are playing on an \(n\times n\) board, and they notice that some patterns are unsolvable. Can you find a rule to decide when a pattern is not solvable?
Suppose that \(x_1+y_1\sqrt{d}\) gives a solution to Pell’s equation \(x^2-dy^2=1\). Define a sequence \(x_n+y_n\sqrt{d} = (x_1+y_1\sqrt{d})^n\). Show that we have the recurrence relations \(x_{n+2} = 2x_1x_{n+1}-x_n\) and \(y_{n+2} = 2x_1y_{n+1}-y_n\).
Prove that the only solution to \(5^a-3^b=2\) with \(a,b\) being positive integers is \(a=b=1\).
Show that Pell’s equation \(x^2-dy^2=1\) has a nontrivial solution.