Problems
How many \(10\)-digit numbers are there such that the sum of their digits is \(3\)?
We want to prove Monsky’s theorem as a corollary of Sperner’s lemma:
it is not possible to dissect a square into an odd number of triangles
of equal area. After scaling we can consider the square with
coordinates: \((0,0),(0,1),(1,0),(1,1)\), which we want to
cut into \(n\) triangles with area
\(\frac{1}{n}\) each for an odd \(n\). Consider the following coloring of all
the points with rational coordinates \((\frac{p}{q},\frac{r}{s})\) inside the
square:
We look at the powers of \(2\) in the
fractions \((\frac{p}{q},\frac{r}{s})\), first of all
the numbers \(p,q\) are coprime, and
thus only one of them is divisible by \(2\), same with \(r,s\). Then the following possibilities
might occur:
Neither \(q\) nor \(s\) is divisible by \(2\). In this case we color the point red.
\(\frac{r}{s}\) is divisible by a larger or equal power of \(2\) than \(\frac{p}{q}\) and \(p\) is not divisible by \(2\). In this case we color the point blue.
\(\frac{p}{q}\) is divisible by a strictly larger power of \(2\) than \(\frac{r}{s}\) and \(r\) is not divisible by \(2\). In this case we color the point green.
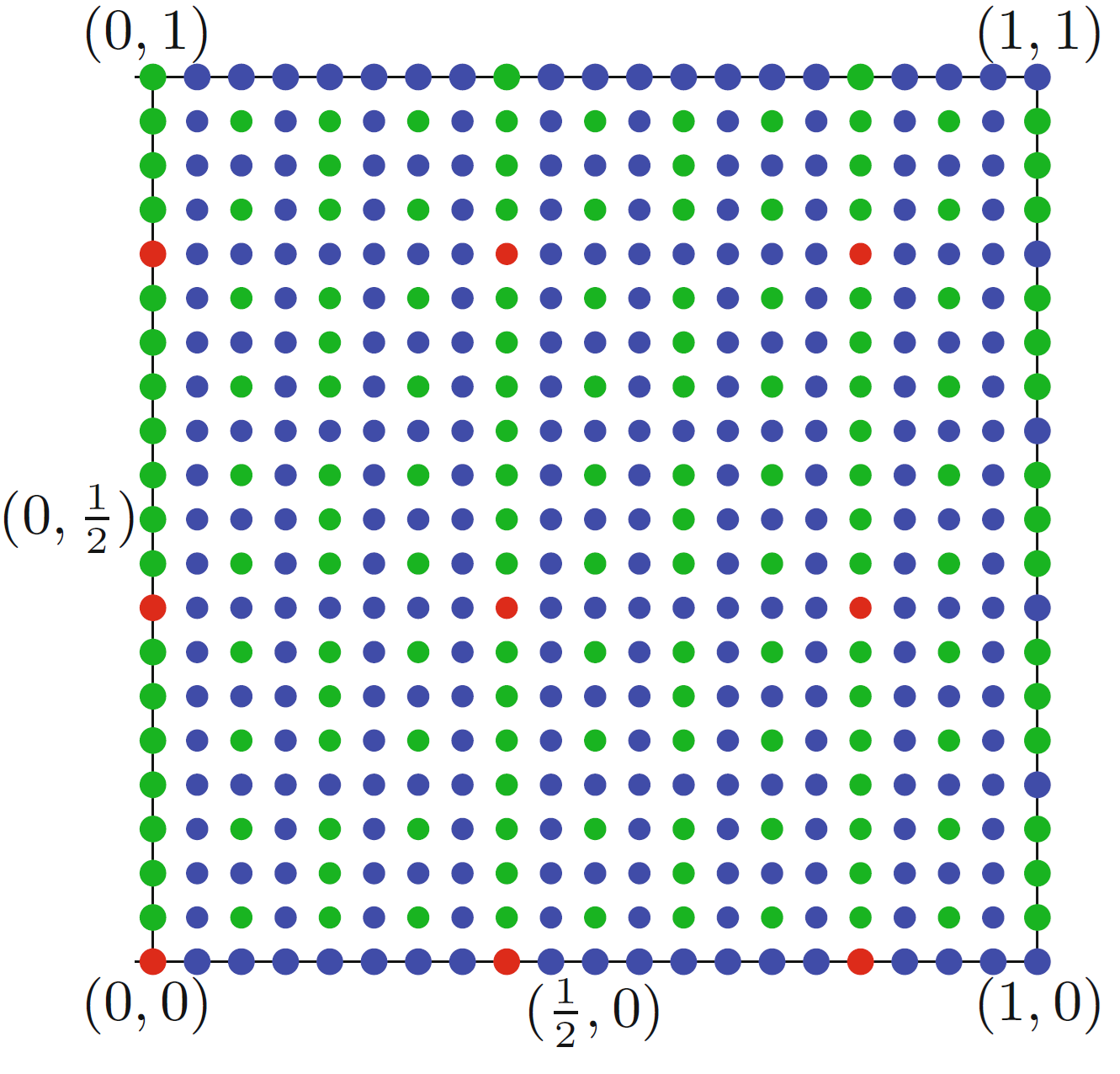
Under an assumption (which you do not have to prove) that the area of any rainbow triangle is at least \(\frac{1}{2}\) prove the Monsky’s theorem.
The sum of digits of a positive integer \(n\) is the same as the number of digits of \(n\). What are the possible products of the digits of \(n\)?
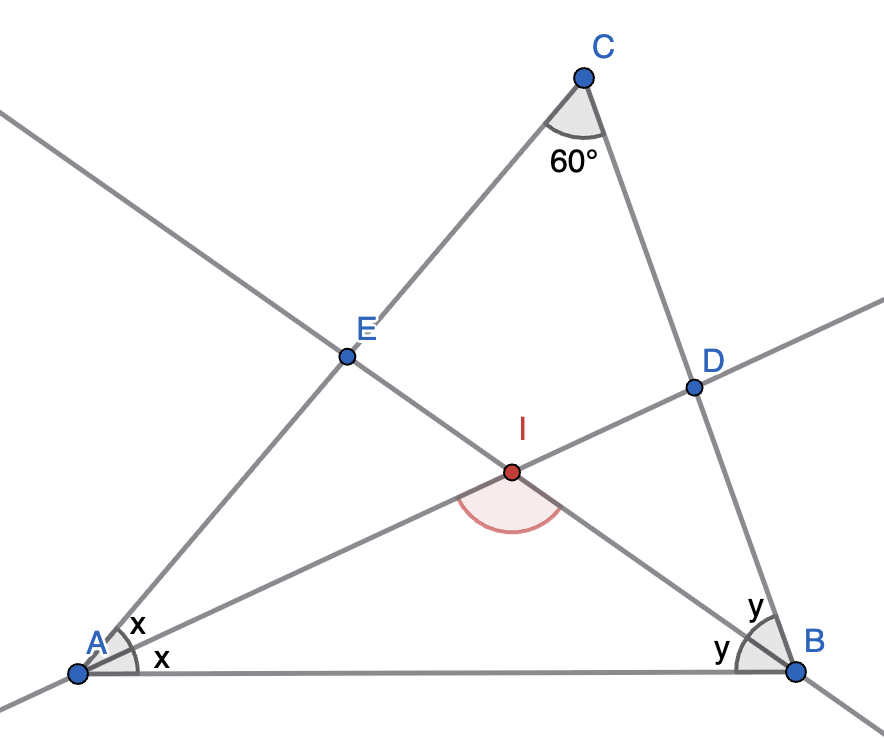
In the triangle \(\triangle ABC\), the angle \(\angle ACB=60^{\circ}\), marked at the top. The angle bisectors \(AD\) and \(BE\) intersect at the point \(I\).
Find the angle \(\angle AIB\), marked in red.
Find, with proof, all integer solutions of \(a^3+b^3=9\).
Prove the general version of Sperner’s lemma: Consider an \(n\)-dimensional simplex \(\mathcal{A} = A_1A_2...A_{n+1}\). Strictly speaking a simplex is a convex linear combination of \(n+1\) points in general position (when \(k\) points are never in one subspace of dimension \(k-1\)). One can view it as an \(n\)-dimensional tetrahedron or a body spanned over vertices \((0,0,...,0), (1,0,0,...,0), (0,1,0,0...,0), ... (0,0,...0,1)\). \[\mathcal{A} = \{\sum_{i=1}^{n+1}a_i(0,0,...,1,...,0), \,\,\, a_i \geq 0, \,\,\,\, \sum_{i=1}^{n+1}a_i = 1\}.\]
A simplicial subdivision of an \(n\)-dimensional simplex \(\mathcal{A}\) is a partition of \(\mathcal{A}\) into small simplices (cells)
of the same dimension, such that any two cells are either disjoint, or
they share a full face of a certain dimension.
Define a Sperner’s coloring of a simplicial subdivision as an assignment
of \(n+1\) colors to the vertices of
the subdivision, so that the vertices of \(\mathcal{A}\) receive all different colors,
and points on each face of \(\mathcal{A}\) use only the colors of the
vertices defining the respective face of \(\mathcal{A}\).
Prove that every Sperner’s coloring of any subdivision of an \(n\)-dimensional simplex contains an odd
number of rainbow simplexes, namely whose vertices are colored using all
\(n+1\) colors.
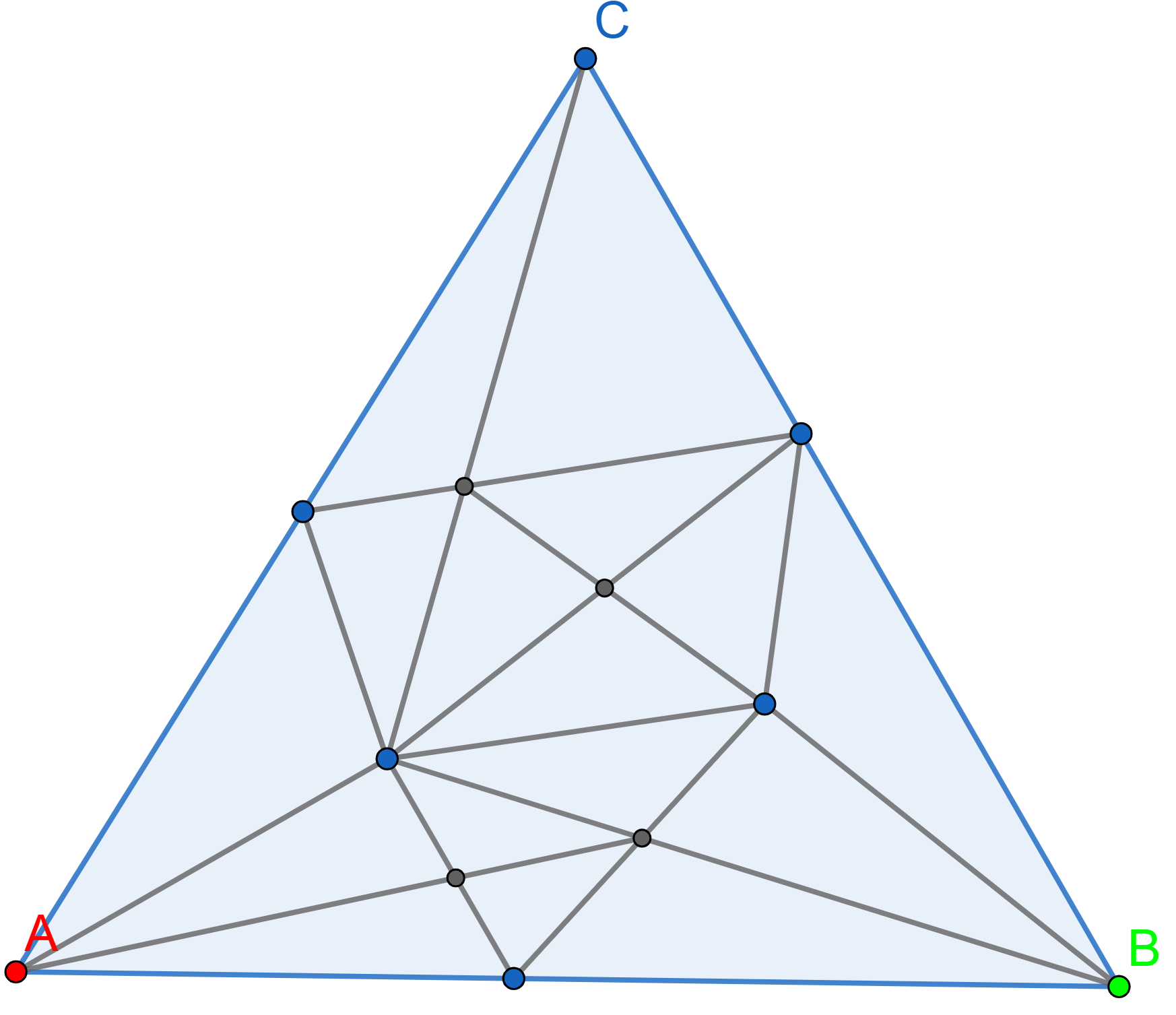
Draw Sperner’s coloring for the following triangulation. Try to avoid rainbow triangles at all costs.
Consider an \(n\)-dimensional simplex \(\mathcal{A} = A_1A_2...A_{n+1}\), namely a body spanned over vertices \((0,0,...,0), (1,0,0,...,0), (0,1,0,0...,0), ... (0,0,...0,1)\). \[\mathcal{A} = \{\sum_{i=0}^{n}a_i(0,0,...,1,...,0), \,\,\, a_i \geq 0, \,\,\,\, \sum_{i=1}^{n+1}a_i = 1\}.\] Where next to \(a_i\) there is a point with coordinate where \(1\) is in \(i\)-th place. The point \((0,0,...,0)\) belongs to the simplex as well.
A simplicial subdivision of an \(n\)-dimensional simplex \(\mathcal{A}\) is a partition of \(\mathcal{A}\) into small simplices (cells)
of the same dimension, such that any two cells are either disjoint, or
they share a full face of a certain dimension.
Define a Sperner’s coloring of a simplicial subdivision as an assignment
of \(n+1\) colors to the vertices of
the subdivision, so that the vertices of \(\mathcal{A}\) receive all different colors,
and points on each face of \(\mathcal{A}\) use only the colors of the
vertices defining the respective face of \(\mathcal{A}\).
Consider a simplicial subdivision given by pairwise connected middles of
all the segments in the original simplex. Assign the numbers \(0,1,2...,n\) to the subdivision vertices in
such a way as to conduct a Sperner’s coloring in such a way that you
will have only one rainbow simplex.
Consider an equilateral triangle \(ABC\). Parallel to each side, five equally spaced segments are drawn across the triangle so that \(ABC\) is subdivided into \(36\) smaller equilateral triangles. Vertices \(A,B\) and \(C\) are painted red, blue and green, respectively in counterclockwise order. Alice and Bob take turns painting each vertex of the smaller triangles either red, green, or blue with the following restrictions: the segment \(AB\) can only have red or green, the segment \(BC\) can only have green and blue, and the segment \(AC\) can only have blue and red. The interior vertices can be drawn freely. Once all vertices have been painted, Alice gets a point for every smaller triangle whose vertices have the three colors (red, green, and blue) appearing in the counterclockwise direction. Bob gets a point for every smaller triangle whose vertices have the three colors but in the clockwise direction. Who wins?
An equation of the form \(x^2 - dy^2 = 1\) where \(d>0\) is a nonsquare (what if \(d\) is a square?) integer and we seek \(x,y\) in the integers is called Pell’s equation. By changing the sign of \(x\) and \(y\), we may assume they are nonnegative. There is always the solution \((x,y)=(1,0)\) which we call trivial.
Here is a useful way to think about the solutions to Pell’s equations. The difference of squares identity prompts us to consider the solution \((x,y)\) to Pell’s equation as the real number \(x+y\sqrt{d}\). The fact that \((x,y)\) is a solution simply means \((x+y\sqrt{d})(x-y\sqrt{d})=1\).
Here is some common notation you might see if you look at books or on the internet: if we have a number \(u=x+y\sqrt{d}\), we can define its conjugate as the number \(\bar u=x-y\sqrt{d}\). Moreover, the set of numbers of the form \(x+y\sqrt{d}\) where \(x,y\) are whole numbers, is often written as \(\mathbb Z[\sqrt{d}]\) (pronounced “integers adjoint \(\sqrt{d}\)"). Therefore, a number \(u\) that belongs to \(\mathbb Z[\sqrt{d}]\) is a solution to Pell’s equation if \(u\bar u=1\).
As with all Diophantine equations, we would like to to know the following about Pell’s equation.
Does Pell’s equation always have nontrivial solutions?
When Pell’s equation does have solutions, is the number of solutions finite?
How can we describe all solutions to Pell’s equation?
In this sheet, we answer all of the questions above and apply these theoretical results to some other problems.