Problems

Let \(A,B,C,D\) be points on the plane represented by complex numbers \(a,b,c,d\). Show that the segments \(AB\) and \(CD\) are perpendicular if and only if \[\frac{d-c}{b-a}=-\frac{\bar d-\bar c}{\bar b- \bar a}\]

Draw some points \(a,b,c\) in the complex plane (whichever you like), and then draw the points \(ia, ib, ic\). Do you notice what geometric action corresponds to multiplying by \(i\)? Can you prove that this is the case?

Let \(a,b\) be complex numbers with \(|a|=|b|=1\). Let \(z\) some other complex number. Show that the reflection of \(z\) about the line that connects \(a\) and \(b\) is given by \[a+b-ab\bar z\]

Let \(\ell\) be a line in the complex plane through the origin. Show that multiplication by a complex number sends \(\ell\) into another line through the origin.

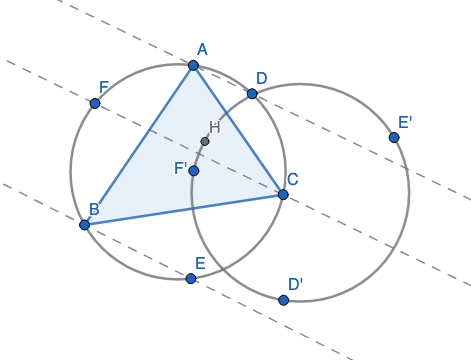
Let \(H\) be the orthocenter of triangle \(\triangle ABC\) (i.e: the point where the three heights meet). Let \(D,E,F\) be three points on the circumcircle of \(\triangle ABC\) such that lines \(\overline{AD}, \overline{FC}, \overline{BE}\) are all parallel to each other. Then, let \(D',E',F'\) be obtained by reflecting \(D,E,F\) across \(BC,CA,AB\) respectively. Prove that the points \(H,D',E',F'\) all lie on the same circle.

A \(5\times5\) grid is given with \(25\) counters, each red on one side and white on the other. Counters are placed on the grid one at a time. When a counter is placed, any counters on neighbouring squares are flipped. Two squares are neighbours if they share a side (not just a corner). The aim is to finish with all counters showing red. During the process counters may flip several times. How many flips occur in total?

The entire plane is coloured using two colours: red and blue. Prove that there must exist two points of the same colour that are exactly \(1\) meter apart.

Give a visual proof that the sum of consecutive numbers until \(n\), i.e: \(1+2+\cdots + n\), where \(n\) is some whole number; is equal to \(n(n+1)/2\).

Use a visual proof to find the value of \[\frac{1+3+5+\cdots +2n-1}{(2n+1)+(2n+3)+\cdots + (4n-1)}\] You are not allowed to use the result from the examples to simplify the fraction.

The Pythagorean Theorem is a very useful tool in geometry. It says that if you have a right-angled triangle with sides measuring \(a,b,c\) where \(c\) is the longest side of the three, then \(a^2+b^2=c^2\). Explain how the following diagram gives a visual proof of the Pythagoraen Theorem.