Problems
Varoon and Mahmoud are given two plates of fruit. On one plate, there are \(13\) apples, on the other, there are \(16\) pears. Each of the boys can take any number of fruit from one plate when he moves. The person who takes the last fruit wins. If Mahmoud starts, who will win?
This time, Sally and Fatima have some number of books on a shelf. Every turn, each of them is allowed to take 1, 3 or 4 books from the shelf. The girl that takes the last book wins, Sally goes first. Who will win if there are: a) 14, b) 16, c) 19 books on the shelf?
Danny and Robbie draw diagonals of a regular \(2018\)-gon. They can only draw a diagonal that does not cross any other diagonal that has been already drawn, neither it begins nor ends at a same point as any other drawn diagonal. Robbie starts – can he always win?
Adam and Anthony are playing with a chessboard and a rook. The rook can only be moved either to the bottom or to the left. Each of the boys can move it as far as he wants, but only in a straight line either to the bottom or to the left. The boy who places the rook in the bottom left corner wins. Adam starts, show that he can lose to Anthony only if the rook starts somewhere on the main diagonal.
Nathan and Liam have numbers from \(1\) to \(2018\) written on a board. In each move, one of the players removes a number of their choosing, which is still on the board, together with all its remaining divisors. Liam goes first. The last person to remove a number wins. Who has the winning strategy?
Alex and Priyanka have a chessboard and a queen on it. Each of the players can only move the queen to the top, to the right, or along a diagonal – to the top and right (like the queen moves, but only in three directions out of all eight). The person who places the queen in the top right corner wins. The chessboard is a normal \(8 \times 8\) board. The queen starts four squares to the right from the bottom left corner. If Priyanka starts, who will win the game?
Orcs and goblins, 40 creatures altogether, are standing in a rectangular formation of \(4\) rows and \(10\) columns. Is it possible that the total number of orcs in each row is \(7\), while the number of orcs in each column is the same?
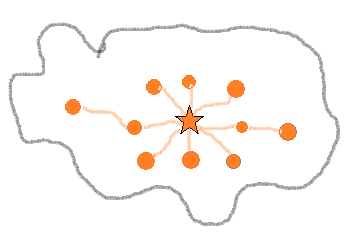
There are some cannons in every fortress on Cannon Island. The star marks the Grand Fortress, the capital, and the \(10\) circles mark \(10\) smaller fortresses. The total number of cannons located in all the fortresses along the east-west road is known to be \(130\). The total number of cannons along each of the other three roads is \(80\). Also it is known that there is a total of \(280\) cannons in all the fortresses. How many cannons are in the capital?
There are \(5\) directors of \(5\) banks sitting at the round table. Some of these banks have a negative balance (they owe more money than they have) and some have a positive balance (they have more money than they owe). It is known that for any 3 directors sitting next to each otehr, their 3 banks together have a positive balance. Does this mean that the \(5\) banks together have a positive balance?
A group of Martians and a group of Venusians got together for an important talk. At the start of the meeting, each Martian shook hands with 6 different Venusians, and each Venusian shook hands with 8 different Martians. It is known that 24 Martians took part in the meeting. How large was the delegation for Venus?