Problems
A \(3 \times 3\) magic square is a square with different number from \(1\) to \(9\) in each of its \(9\) cells. The numbers in each row, column and diagonal sum up to \(15\). Show that there is a number \(5\) in the centre of the square.
Can you decorate an \(8 \times 8\) cake with chocolate roses in such a way that any \(2 \times 2\) piece would have exactly 2 roses on it, and any \(3 \times 1\) piece would have exactly one rose? Either draw such a cake or explain why this is not possible.
Several films were nominated for the “Best Math Movie“ award. Each of the 10 judges secretly picked the top movie of their choice. It is known that out of any 4 judges, at least 2 voted for the same film. Prove that there exists a film that was picked by at least 4 judges.
Out of \(7\) integers, the sum of any \(6\) is a multiple of \(5\). Show that every one of these numbers is a multiple of \(5\).
An \(8 \times 8\) chessboard has 30 diagonals total (15 in each direction). Is it possible to place several chess pieces on this chessboard in such a way that the total number of pieces on each diagonal would be odd?
Anna’s garden is a \(n \times m\) grid of squares. She wants to have trees in some of these squares, but she wants the total number of trees in each column and in each row to be an odd number (not necessarily the same, they just all need to be odd). Show that it is possible only if \(m\) and \(n\) are both even or both odd and calculate in how many different ways she can place the trees in the grid.
Matt built a simple wooden hut to protect himself from the rain. From the side the hut looks like a right triangle with the right angle at the top. The longer part of the roof has 20 ft and the shorter one has 15 ft. What is the height of the hut in feet?
The three sides of a right triangle have all integer lengths. Show that at least one of them has an even length.
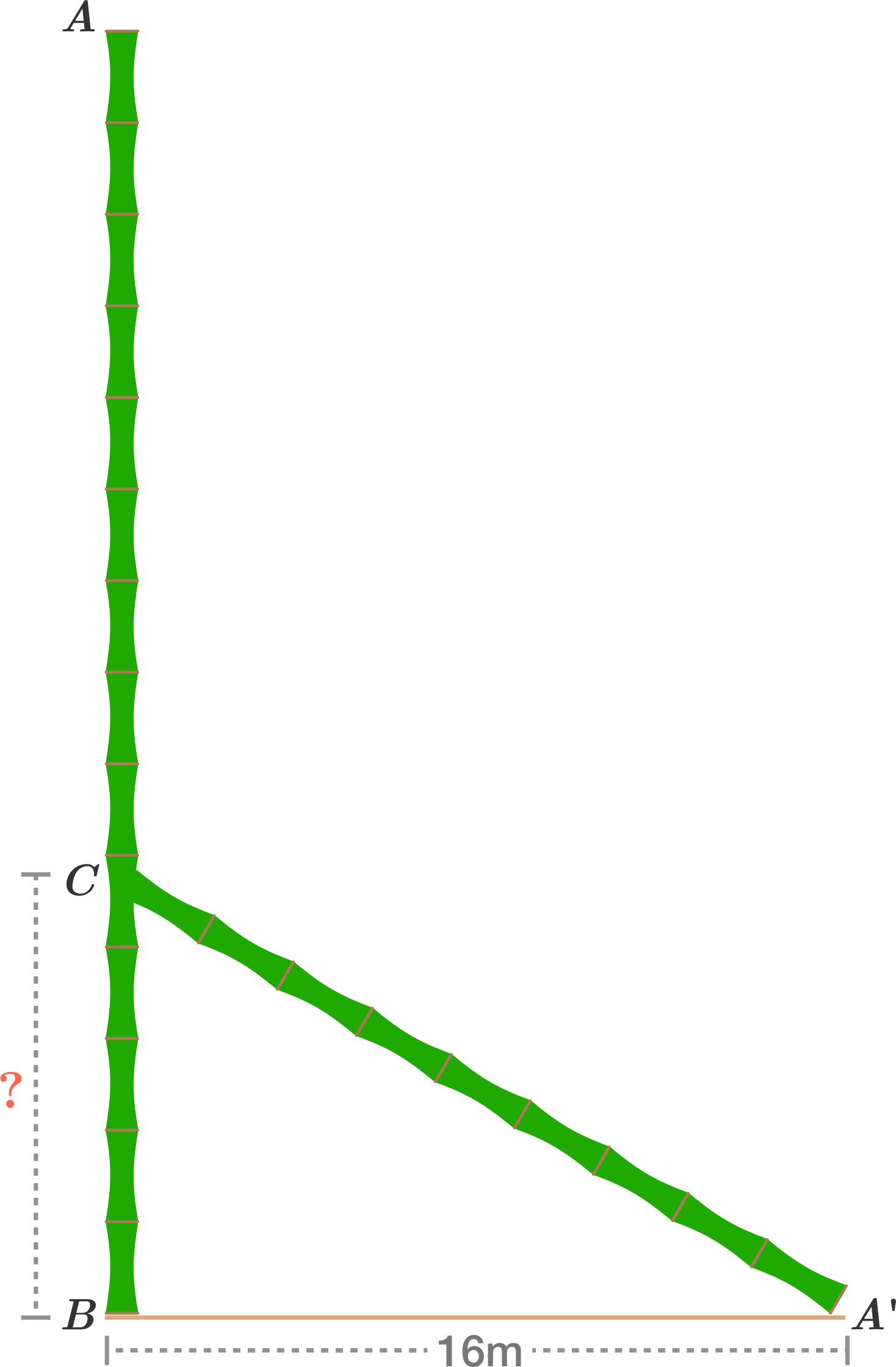
A bamboo tree, originally \(32\) metres high, broke in two parts. The end of the other one has fallen \(16\) metres away from the trunk. How high is the remaining vertical part of the bamboo tree?
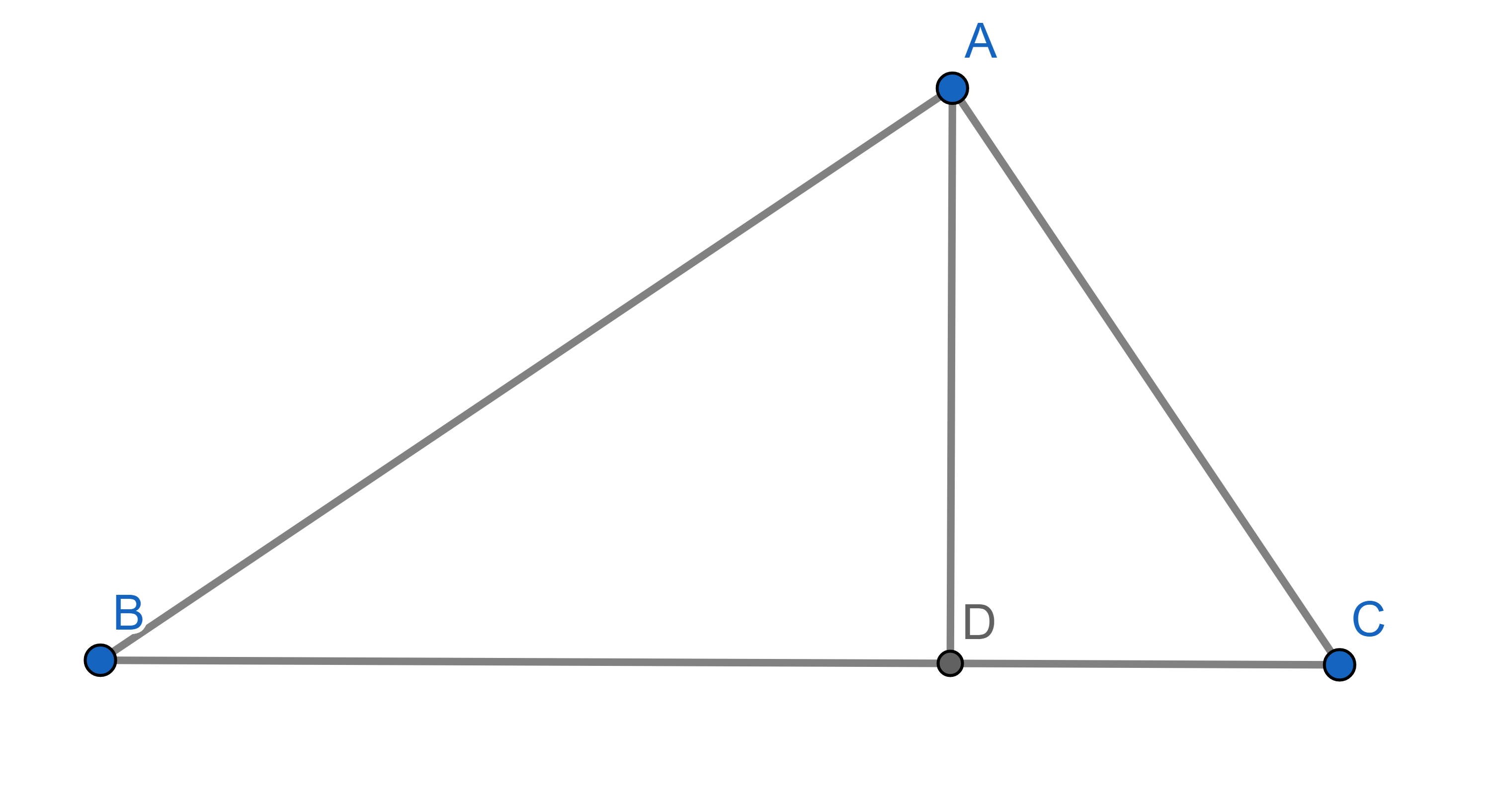
Matt has built an additional support for his hut (\(AD\)), whose length is \(12\)ft, and the base \(BC\) is \(25\)ft. We also know \(AB = 20\) and \(AC = 15\). What are the distances \(|BD|\) and \(|DC|\)? Show that \(|AD|^2=|BD| \times |AC|\) in this particular case. Do you think it is true in general?