We solve problems

Problems Algorithm Theory Theory of algorithms (other) Discrete Mathematics

There are 6 locked suitcases and 6 keys to them. At the same time, it is not known to which suitcase each key fits. What is the smallest number of attempts you need to make in order to open all the suitcases for sure? And how many attempts will it take there are not 6 but 10 keys and suitcases?

Problem #PRU-103027

Problems Algorithm Theory Theory of algorithms (other) Discrete Mathematics

10–12 2.0

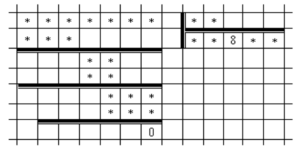
Decipher the following rebus (see the figure). Despite the fact that only two figures are known here, and all others are replaced by asterisks, the example can be restored.

Problem #PRU-103729

Problems Divisibility Odd and even numbers Number Theory

10–12 2.0

The parliament of a certain country has two houses with an equal number of members. In order to make a decision on an important issue all the members voted and there were no abstentions. When the chairman announced that the decision had been taken with a 23-vote advantage, the opposition leader declared that the results had been rigged. How did he know it?

Problem #PRU-103738

Problems Union, intersection, and set difference Discrete Mathematics Set theory and logic Set theory

11–12 2.0

Among some number of mathematicians, every seventh is a philosopher, and among some number of philosophers every ninth is a mathematician. Who are there more of: philosophers or mathematicians?

Problem #PRU-103749

Problems Methods Order relations Pigeonhole principle Pigeonhole principle (other) Discrete Mathematics Set theory and logic

10–12 2.0

Know-it-all came to visit the twin brothers Screw and Nut, knowing that one of them never speaks the truth, and asked one of them: “Are you Screw?”. “Yes,” he replied. When Know-it-all asked the second brother the same question, he received an equally clear answer and immediately determined who was who.

Who was called Screw?

Problem #PRU-103757

Problems Algebraic equations and systems of equations Algebra Higher order equations. Palindromic polynomial equations Equations of higher order (other) Real numbers Integer and fractional parts. Archimedean property Calculus

12–14 2.0

A resident of one foreign intelligence agency informed the centre about the forthcoming signing of a number of bilateral agreements between the fifteen former republics of the USSR. According to his report, each of them will conclude an agreement exactly with three others. Should this resident be trusted?

Problem #PRU-103780

Problems Methods Algebraic methods Partitions into pairs and groups; bijections Proof by exhaustion Pigeonhole principle Pigeonhole principle (other)

11–13 3.0

In any group of 10 children, out of a total of 60 pupils, there will be three who are in the same class. Will it always be the case that amongst the 60 pupils there will be: 1) 15 classmates? 2) 16 classmates?

Problem #PRU-103781

Problems Fun Problems Word Problems

11–12 2.0

A pedestrian walked along six streets of one city, passing each street exactly twice, but could not get around them, having passed each one only once. Could this be?

Problem #PRU-103787

Problems Methods Algebraic methods Counting in two ways Extremal principle Extremal principle (other) Pigeonhole principle Pigeonhole principle (other)

12–14 3.0

One term a school ran 20 sessions of an after-school Astronomy Club. Exactly five pupils attended each session and no two students encountered one another over all of the sessions more than once. Prove that no fewer than 20 pupils attended the Astronomy Club at some point during the term.

Problem #PRU-103791

Problems Puzzles Numeral systems Decimal number system Number Theory Discrete Mathematics Set theory and logic Mathematical logic

12–12 3.0

In the rebus below, replace the letters with numbers such that the same numbers are represented with the same letter. The asterisks can be replaced with any numbers such that the equations hold.

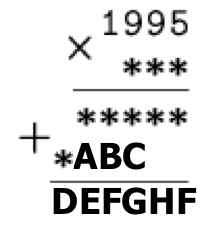
An explanation of the notation used: the unknown numbers in the third and fourth rows are the results of multiplying 1995 by each digit of the number in the second row, respectively. These third and fourth rows are added together to get the total result of the multiplication \(1995 \times ***\), which is the number in the fifth row. This is an example of a “long multiplication table”.